Introducción al algoritmo PID y su implementación en Arduino
Introducción
Actualmente, el controlador PID se erige como el método dominante en la ingeniería de control de procesos. Su extraordinaria popularidad se debe a varias razones, pero, ¿qué lo distingue realmente? ¿Cómo ha alcanzado este algoritmo tal grado de omnipresencia que una búsqueda rápida en Google arroja más de dos mil millones de resultados? La respuesta es más sencilla de lo que parece: el PID es un algoritmo tanto elemental como resistente. Su robustez es tal que incluso un novato en el ajuste de parámetros de sintonía puede lograr un control razonablemente bueno con un conocimiento básico. La importancia de este algoritmo es innegable; se utiliza cada vez que se activa un control de crucero en un vehículo, cada vez que un piloto enciende el piloto automático, y cada vez que se imprime un objeto en una impresora 3D.
El objetivo de este artículo es ofrecer una introducción al algoritmo PID y proporcionar al lector una gama de conceptos y técnicas analíticas simples que faciliten la implementación de un controlador PID. Aunque el enfoque está en Arduino, las estrategias y principios descritos son aplicables a cualquier microcontrolador económico capaz de soportar un PID digital.
Terminología
A menudo se utiliza una gran variedad de terminología asociada a los PIDs que confunde enormemente al lector en las primeras tomas de contacto con este mundillo. A continuación una lista de la terminología que considero básica:
- Kc: Ganancia proporcional del controlador.
- Ti: Tiempo integral del controlador. No confundir con Ki. En este caso, a mayor tiempo integral más lento corregimos el Error.
- Td: Tiempo derivativo del controlador. No confundir con Kd. Es el término más incomprendido y difícil de ajustar, de momento quedaros con la idea de que el tiempo derivativo actúa sobre la velocidad de cambio del error.
- Ki: Ganancia integral del controlador. Cuanto mayor es la ganancia, más rápido corregimos el Error. Si hubiera que convertir tened en cuenta que Ki = Kc/Ti.
- Kd: Ganancia derivativa del controlador. Si hubiera que convertir tened en cuenta que Kd = Kc*Td.
- Ku: Ganancia última.
- Tu: Periodo de oscilación mantenida.
- PV: Son las siglas de Process Variable, es decir, variable de proceso.
- SP: Son las siglas de Set Point, es decir, punto de consigna. Es el punto donde queremos llevar a la variable de proceso.
- OP: En inglés Output, es decir, la salida. Es lo que «movemos» para alterar la variable de proceso.
- Error: Es la diferencia entre PV y SP. Error = PV-SP o Error = SP-PV.
- K o Kp: Ganancia del proceso. Es la ganancia representativa del proceso que estamos estudiando obtenida mediante técnicas en lazo abierto como el de la curva de reacción o similar.
- T0: Tiempo muerto del proceso. Es el tiempo entre que se mueve la OP y lo nota la PV.
- TP: Tiempo de proceso. Desde que comienza a moverse la PV hasta que alcanza el 63,2% de la respuesta.
- Ts: Tiempo de muestreo.
- Tf: Constante de tiempo deseada en lazo cerrado.
- Lazo abierto: Un proceso está en lazo abierto cuando el controlador se encuentra desconectado del proceso, es decir, el controlador no toma ninguna decisión sobre cómo mantener la variable controlada en su punto de consigna. Por ejemplo, MODO MANUAL de un controlador.
- Lazo cerrado: Un proceso está en lazo cerrado cuando el controlador se encuentra conectado al proceso comparando el valor del punto de consigna con la variable controlada y determinando la acción correctiva necesaria. Por ejemplo, MODO AUTOMÁTICO de un controlador.
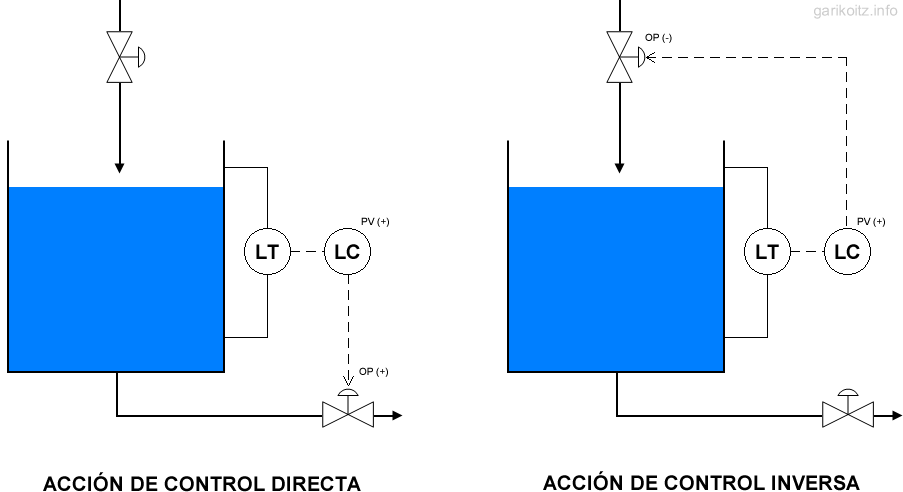
- Acción de control: Es la «forma de trabajar» de nuestro controlador pudiendo ser directa o inversa.
- Directa: Ante un incremento de la PV (+) hay que incrementar la OP (+). Un ejemplo típico es un depósito de agua en el que queremos controlar el nivel y disponemos de una válvula en la salida con la que controlamos el vaciado. En este caso al llegar agua al depósito, el nivel sube y por lo tanto la válvula tendrá que abrir para mantener el nivel anterior.
- Inversa: Ante un incremento de la PV (+) hay que disminuir la OP (-). Si en el ejemplo anterior situamos la válvula en el aporte de agua, si el nivel sube la válvula que ahora regula el agua de entrada tendrá que cerrar.
El algoritmo PID
El algoritmo PID tiene tres mecanismos de control que son Proporcional, Integral y Derivativo. Una característica interesante es que cada término es independiente y se puede ajustar por separado.
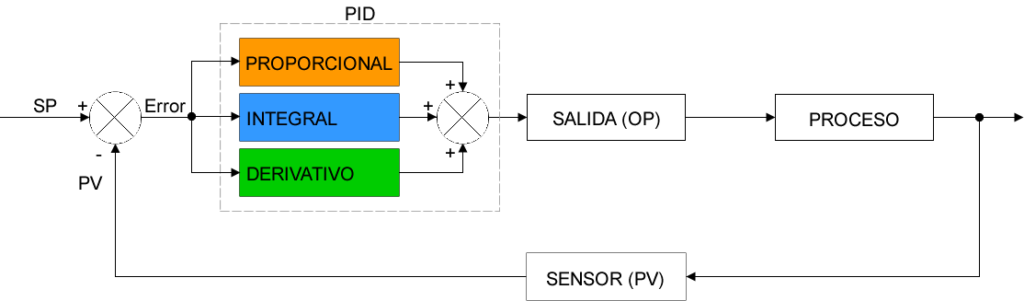
Cada mecanismo del PID trabaja de una forma determinada para corregir el error, de modo que:
- El término proporcional (Kc): actúa directamente sobre el error.
- El término integral (Ti): actúa a una velocidad proporcional al error.
- El término derivativo (Td): actúa sobre la velocidad de cambio del error.
Término Proporcional
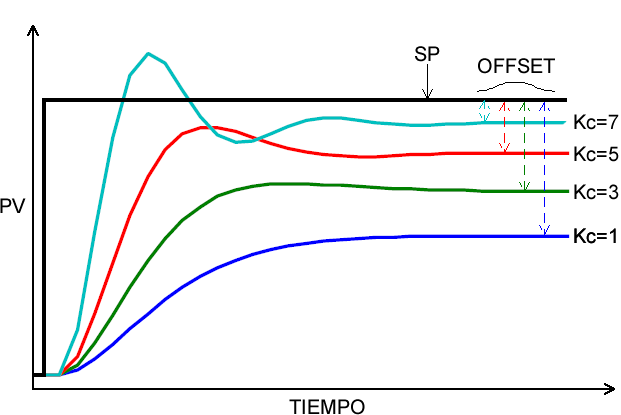
El término proporcional actúa de forma proporcional al error (PV-SP). A mayor ganancia del controlador, menor es el error de offset pero el lazo puede volverse inestable.
En el siguiente vídeo se muestra una simulación de un controlador con término únicamente proporcional. El valor alto del término integral (9999999) es para anularlo ya que el simulador no admite poner un cero.
Término Integral
Es el tiempo en que el controlador alcanza una respuesta (delta de OP) de magnitud similar al error. La acción integral se combina con la proporcional para eliminar el offset. Cuanto menor es Ti más rápido corregimos el error y más agresiva es la respuesta.
Partiendo de la simulación anterior, veamos el efecto de introducir el término integral pasando de un controlador P a uno PI.
Término Derivativo
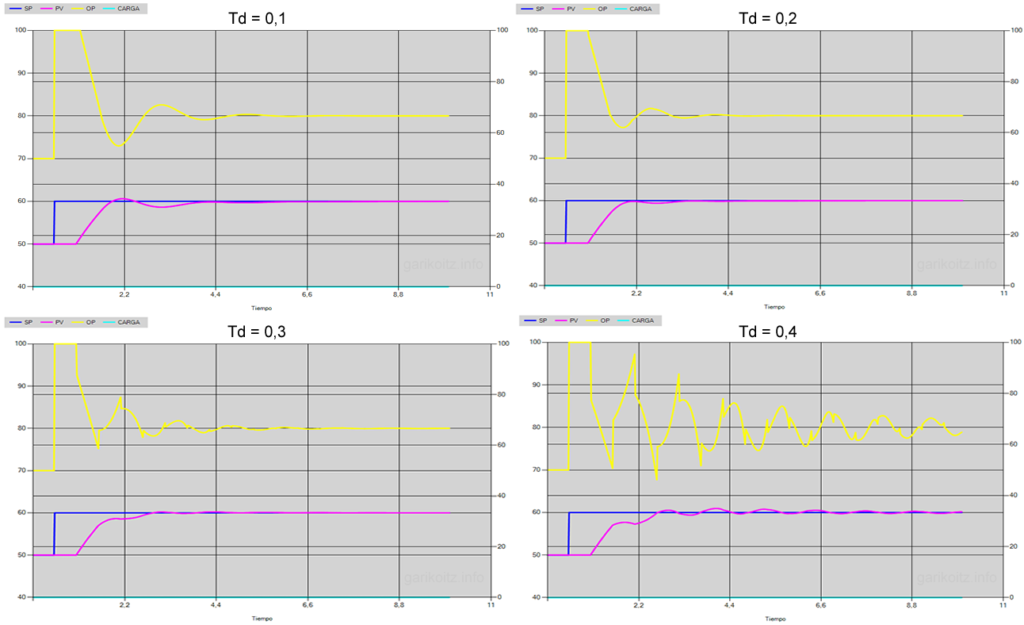
La acción derivativa es independiente del valor absoluto de la medida y se mueve a la velocidad de cambio del error en el tiempo, es decir, se anticipa al cambio del proceso porque actúa según la velocidad de cambio del error. La respuesta es rápida pero no es aconsejable en procesos con ruido. Cuanto mayor es Td más agresivo es el control.
Partiendo de la simulación anterior, veamos el efecto de introducir el término derivativo pasando de un controlador PI a uno PID.
Resumen
Respuesta del término Proporcional
- Un controlador proporcional produce una respuesta inmediata y específica.
- La delta de OP es proporcional a la delta del error y la amplitud se magnifica a mayor ganancia.
- En lazo cerrado queda un error permanente llamado offset.
- El offset se puede reducir aumentando la ganancia pero no se anula.
Respuesta del término Integral
- Actúa siempre que exista error y responde según la magnitud y signo del error a lo largo del tiempo.
- Elimina el error permanente (offset).
- A menor tiempo integral (Ti) mayor acción integral.
Respuesta del término Derivativo
- Ante cambios de SP, la acción derivativa produce un pico en la respuesta (derivative kick). Por este motivo se usa la ecuación PI-D en vez de la clásica PID (ver apartado de ecuaciones).
- No sirve como única respuesta porque solo distingue variaciones del error y no de valores de SP.
- No se aconseja su uso en procesos con ruido.
- A mayor tiempo derivativo (Td) mayor acción derivativa.
Ecuaciones
Si descomponemos el PID en términos independientes y alteramos la afección que tendrá cada término al error y a la PV, digamos que disponemos de varias combinaciones posibles y que cada combinación tiene sus pros y contras. Las más habituales que nos podemos encontrar son PID, PI-D e I-PD siendo las más utilizadas PI-D e I-PD.
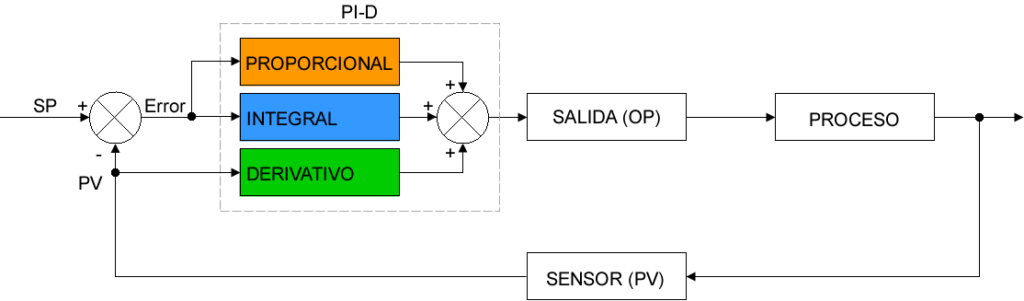
PI-D
El guion que separa los términos indica que los términos proporcional e integral actúan sobre el error y el término derivativo sobre la PV. Esto se hace para evitar el pico que genera la acción derivativa ante un cambio en el SP. Normalmente cuando se habla de la implementación de un PID en realidad lo que se está implementando es la ecuación PI-D. Esta ecuación es adecuada para cambios frecuentes en el SP.
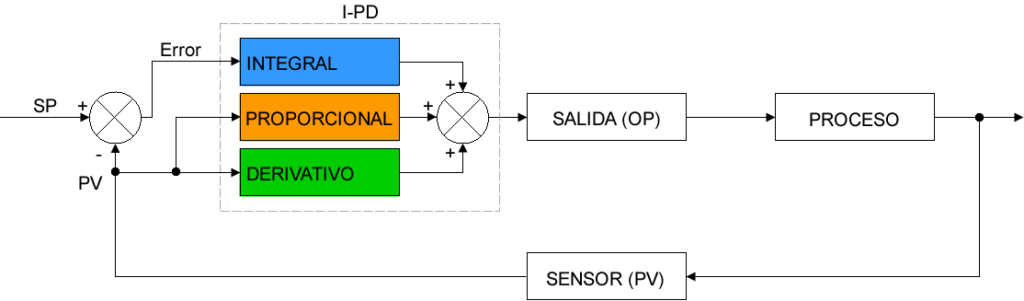
I-PD
En este caso, el término integral actúa sobre el error y los términos proporcional y derivativo sobre la PV. El no afectar el error al término proporcional hace que la respuesta del controlador sea mucho más suave. Esta ecuación es adecuada para rechazo de perturbaciones.
PI-D vs I-PD
Para que quede claro el efecto de las ecuaciones, veamos la diferencia de la respuesta para un mismo proceso partiendo de la simulación anterior.
Tipos de procesos
Respuesta autorregulada
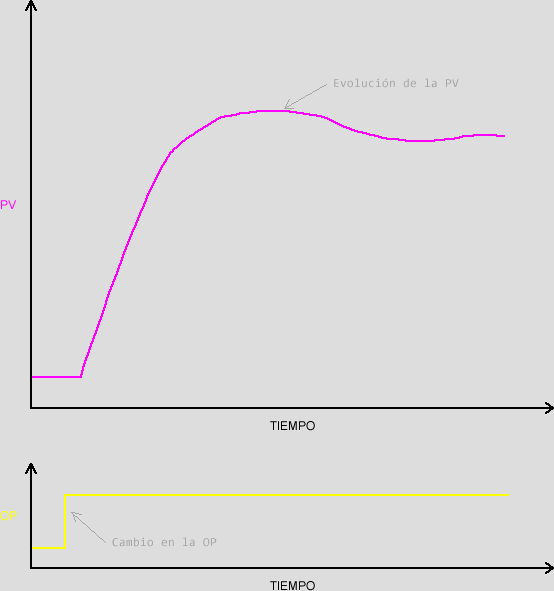
En la respuesta autorregulada, ante una variación de la salida (OP) la variable de proceso (PV) llega a una nueva situación estable. Un ejemplo típico que se puede hacer con Arduino es un control de temperatura en el que estamos controlando con una salida PWM el voltaje de un cartucho calefactor (OP) y que estamos midiendo mediante una sonda de temperatura (PV). Si partiendo de una situación estable aumentamos la salida PWM (OP) pasado un tiempo veremos que la temperatura aumenta y se estabiliza en un nuevo punto como se puede apreciar en la imagen que tenemos a continuación.
Respuesta integral
En la respuesta integral, ante una variación de la salida (OP) la variable de proceso (PV) aumenta o disminuye de manera indefinida. Un ejemplo clásico es un depósito de agua. Si al deposito con el nivel estable (PV) le abrimos el aporte de agua (OP) el nivel aumentará indefinidamente. Otra maqueta típica de Arduino con esta respuesta es el sistema bola-viga.
Identificación de procesos
En lazo abierto
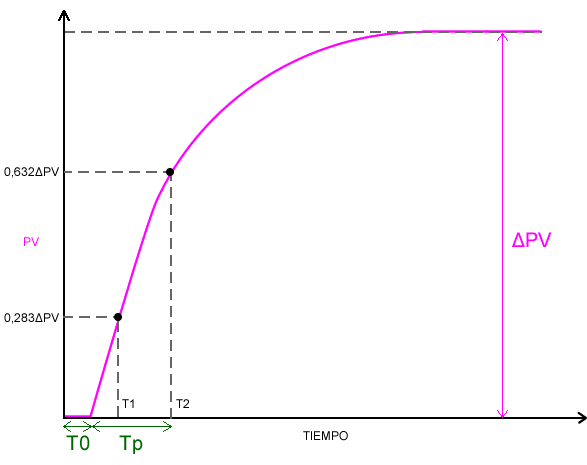
Se trata de caracterizar el proceso de forma simplificada y obtener tres parámetros como son la ganancia del proceso (K o Kp), el tiempo muerto (T0) y el tiempo del proceso (Tp). Una vez obtenidas estas constantes podemos simular en lazo cerrado una gran variedad de sintonías y elegir la que más nos satisfaga.
\begin{align}
& K = \frac{\Delta PV}{\Delta OP}\\
& Tp = 1,5(T2-T1) \\
& T0 = T2-Tp\\
& T1(28,3\%) = PV inicial\pm 0,283\times\Delta PV \\
& T2(63,2\%) = PV inicial\pm 0,632\times\Delta PV
\end{align}Aquí tenéis un par de ejemplos de como calcular las ganancias del proceso [1] [2].
El cociente entre el tiempo muerto (T0) y el tiempo de proceso (Tp) nos da como resultado un valor que sugiere la facilidad de control que tendrá el proceso.
En lazo cerrado
Si las características del proceso nos impidieran realizar un ensayo en lazo abierto, existen dos técnicas en lazo cerrado que nos permiten realizar una identificación para obtener en este caso dos parámetros como son la ganancia última (Ku) y el periodo de oscilación (Tu). Estos parámetros nos permiten calcular un número bastante más limitado de sintonías que las que podemos calcular en lazo abierto.
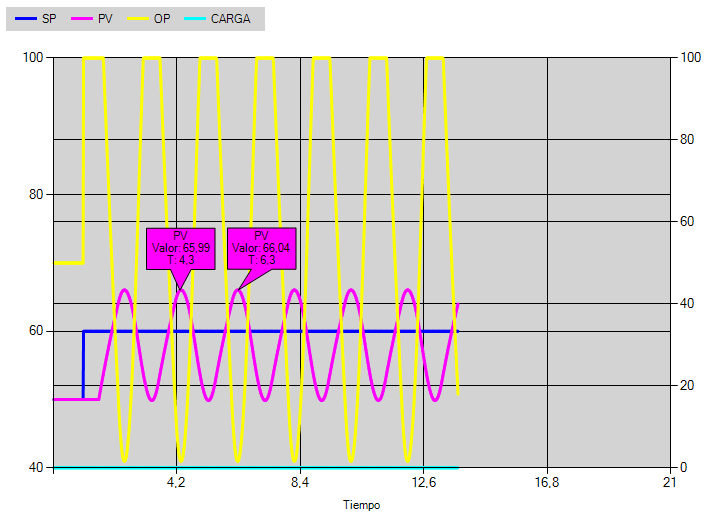
Método de Oscilación Mantenida de Ziegler y Nichols
Este método consiste en implementar un controlador PID con ganancia únicamente proporcional e ir variándola hasta que el sistema entre en oscilación continua. Así obtenemos que Ku es igual a la ganancia proporcional utilizada y Tu es periodo de oscilación. En este caso Ku = 8 y Tu = 2 minutos (6,3-4,3).
Método del relé de Aström y Hägglund
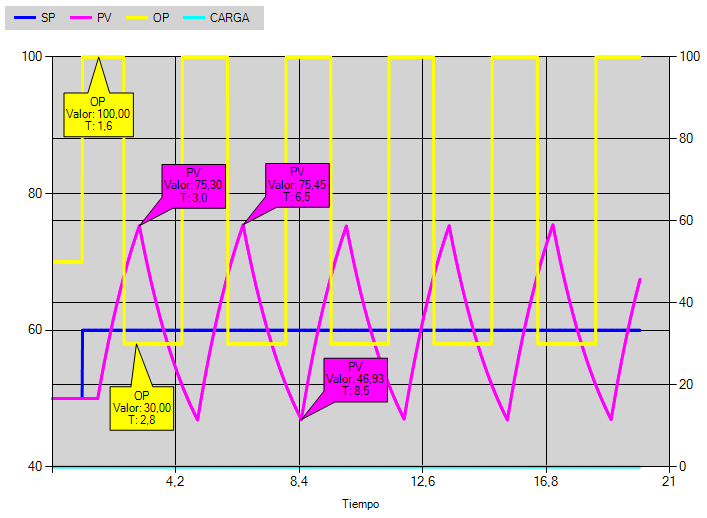
Este método consiste en programar un relé para generar una oscilación mantenida imitando un controlador todo/nada. El relé puede ser con o sin histéresis. Del ensayo obtenemos 3 datos que nos sirven para estimar de nuevo la ganancia última (Ku) y el periodo de oscilación (Tu) como son la amplitud de la PV (a), la amplitud de la OP (d) y el periodo de oscilación (Tc). Se ha usado un relé ideal sin histéresis.
Los datos obtenidos del ensayo son a = 28,52% (75,45-46,93), d = 70% (100-30) y Tc = 3,5 minutos (6,5-3), con los cuales calculamos Ku y Tu.
\begin{align}
& Ku = \frac{4d}{\pi a}=\frac{4\times 70}{\pi\times 28,52}=3,12\\
& Tu = Tc = 3,5 minutos
\end{align}Métodos de sintonía
Prueba y error (Todos los procesos)
- Empezamos únicamente con control proporcional.
- Aumentar Kc en incrementos de un 20% hasta apreciar ligeras oscilaciones.
- Incorporamos la acción integral aumentando Ki en incrementos del 20%. Para compensar el efecto de la acción integral disminuimos Kc.
- Si la respuesta tiene oscilaciones reducir Kc y Ki hasta conseguir la respuesta deseada.
- Incorporamos la acción derivativa con Kd = Ki/4. Al incorporar Kd es necesario ajustar Kc y Ki.
- Ajustar Kc, Ki y Kd hasta conseguir la respuesta deseada ante cambios de SP usando como referencia la tabla que se muestra a continuación.
| Velocidad de respuesta | Estabilidad | Amplificación del ruido | |
| ↑Kc | ↑ | ↓ | ↑ |
| ↑Ki | ↑ | ↓ | ↑ |
| ↑Kd | ↑ | ↑ | ↑↑ |
Modelo K, T0 y TP (Respuesta autorregulada)
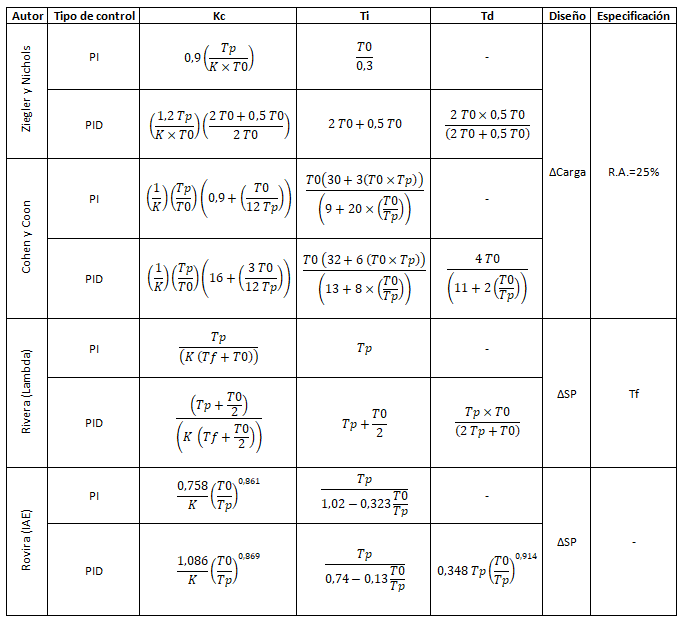
Os dejo una pequeña muestra aunque existe mucha variedad. La columna diseño indica en que situaciones se comporta mejor la sintonía y la columna especificación a lo que esperamos en lazo cerrado. Aquí tenéis una herramienta llamada PIDLab para calcular unas cuantas sintonías más y simular la respuesta en lazo cerrado.
R.A. = 25% significan razón de amortiguamiento también llamado relación de decaimiento del 25%. Esto quiere decir que la respuesta del sistema ante una entrada escalón decae un 25% en el segundo pico. Podéis ver un ejemplo aquí.
Tf es la constante de tiempo deseada en lazo cerrado. Este parámetro es muy interesante ya que nos permite modelar la respuesta de la sintonía.
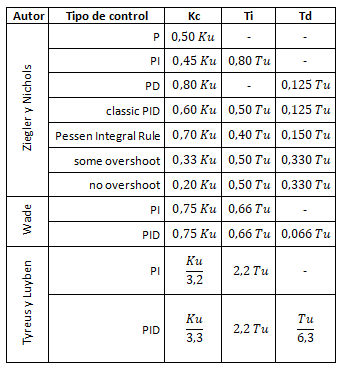
Modelo Ku y Tu (Oscilación mantenida y relé)
Recordad que en las librerías de Arduino se utilizan las ganancias Ki y Kd en lugar de Ti y Td por lo que, Ki = Kc/Ti y Kd = Kc*Td
Inicialización
La inicialización es un concepto muy importante cuando se implementa un PID y que no se suele tener en cuenta en maquetas ‘caseras’. Fundamentalmente, la inicialización implica evitar cambios bruscos en la salida cuando el sistema se cambia al modo automático. Para lograr una transición suave, es esencial precalcular el valor de la salida de control de manera que, al activar el control automático, no empecemos desde cero, lo que podría causar una variación brusca. En cambio, ajustando adecuadamente este valor inicial, el controlador PID puede comenzar a operar más cerca del valor objetivo, reduciendo así el error de manera eficiente y evitando fluctuaciones notables en el proceso.
Adicionalmente a anticipar el valor de la salida de control, es aconsejable implementar una técnica conocida como seguimiento de la variable de proceso (PV Tracking). Esta técnica implica ajustar el punto de ajuste (SP) para que coincida con la variable de proceso (PV) cuando el sistema está en modo manual. De esta manera, al cambiar al modo automático, el error (PV-SP) será cero o muy cercano a cero, asegurando una transición fluida y sin sobresaltos.
Código del PID digital
Implementación teórica
Error = PV - SP P = Error * Kc I = I + Error * Ki D = (Error - Error_Ant) * Kd Error_Ant = Error OP = P + I + D
El código anterior, es una primera aproximación en el que no se tienen en cuenta dos problemas importantes como son el windup y el salto que produce el término derivativo ante un cambio de SP (derivative kick). En aplicaciones reales, ya sean maquetas sencillas o más elaboradas, es necesario implementar al menos esto:
- Anti-windup
- Mínima y máxima OP
- Acción del controlador (directa o inversa)
- Posibilidad de elegir la ecuación del controlador (PI-D, I-PD), o al menos, que el término derivativo trabaje con la delta de PV y no con el error.
Implementación funcional en Arduino
// Asignaciones de pines
const int PIN_PV = A0;
const int PIN_OP = 6;
// Variables
int Ts, maxOP, minOP;
double Kc, Ki, Kd, PV, PVant, dPV, OP, mySP;
String tipo, accion;
// variables internas del controlador
unsigned long TiempoActual, TiempoAnterior;
double TiempoTranscurrido;
double error, error_ant, Pcalc, Ierror, Derror;
//===============================================================
// SETUP
//===============================================================
void setup()
{
PV = analogRead(PIN_PV); // Leemos la PV del pin A0
mySP = 50; // Punto de consigna
Ts = 100; // Tiempo de muestreo
minOP = 0; // Mínimo valor de OP
maxOP = 100; // Máximo valor de OP
accion = "DIRECTO"; // Acción de control
tipo = "PI-D"; // Ecuación
Kc = 1.0;
Ki = 2.0;
Kd = 0.1;
}
//===============================================================
// BUCLE PRINCIPAL
//===============================================================
void loop(){
TiempoActual = millis();
if (millis() - TiempoAnterior >= Ts)
{
PV = analogRead(PIN_PV); // Lectura del sensor
PV = map(PV, 0, 1023, 0, 100); // PV a porcentaje
if(accion == "INVERSO") // Acción de control
{
Kc = (0 - Kc);
Ki = (0 - Ki);
Kd = (0 - Kd);
}
error = mySP - PV;
Ierror += Ki * error;
dPV = (PV - PVant);
if (tipo == "I-PD") Pcalc -= Kc * dPV; // Termino proporcional en función
else Pcalc = Kc * error; // de PI-D o I-PD
if (Ierror > maxOP) Ierror = maxOP; // Anti-windup
else if (Ierror < minOP) Ierror = minOP;
OP = Pcalc + Ierror - Kd * dPV; // Calculamos la salida del PID
if(OP > maxOP) OP = maxOP; // Mínimo y Máximo valor de la OP
else if(OP < minOP) OP = minOP;
PVant = PV; // Guardamos la PV anterior
error_ant = error; // Guardamos el error anterior
TiempoAnterior = TiempoActual; // Guardamos el tiempo anterior
analogWrite(PIN_OP, OP); // Mandamos la salida al pin PWM
TiempoAnterior = millis();
}
}
Librerías disponibles
Para control
- Arduino PID library creada por Brett Beauregard. Probablemente la librería más famosa y utilizada para control PID en Arduino. Dispone de protección anti-windup, permite especificar la acción de control y a partir de la versión 1.2 incluyó la posibilidad de elegir entre las ecuaciones PI-D e I-PD indicando los parámetros P_ON_E y P_ON_M respectivamente. También permite cambiar las variables de sintonía ‘on the fly’ y por supuesto pasar de manual a automático y viceversa mediante código.
- QuickPID creada por Dlloydev. Es una modificación de la librería de Brett Beauregard con alguna protección anti-windup adicional.
- AutoPID creada por Ryan Downing. Dispone de protección anti-windup pero a cambio implementa la ecuación PID clásica por lo que notaremos la famosa derivative kick.
- FastPID creada por Mike Matera. Promete ser más rápido que otras librerías a base de la simplificación interna de los cálculos en coma flotante. Contiene lo básico pero de nuevo peca al implementar la ecuación PID clásica.
Si optáis por usar una librería, cualquiera de las dos primeras es válida. Si vais a usar otra o ya la usáis, comprobad en el código realmente como funciona para que no os llevéis ninguna sorpresa.
Para identificación
- Arduino PID AutoTune Library creada por Brett Beauregard. Implementa el método del relé y nos devuelve un juego de parámetros PI y PID calculados con las reglas de Ziegler y Nichols.
- Arduino PID autotuner creado por Jack01. Implementa el método del relé y sintonías de Ziegler y Nichols. Antes de iniciar el proceso elegimos si queremos que nos devuelva la sintonía «classic PID» o «some overshoot». En caso de que no especifiquemos nos devuelve las más seguras «no overshoot».
- sTune creada por Dlloydev. Realiza un test en lazo abierto mediante el método del punto de inflexión sobre la curva de reacción. La configuración es más exigente y nos obliga a conocer la respuesta de nuestro proceso. Al principio cuesta dar con el funcionamiento de la librería pero como recompensa obtendremos un modelo del proceso mediante K, T0 y Tp y un juego de sintonías. También nos da el factor de controlabilidad que en este caso es inverso a la facilidad de control comentado anteriormente.
Podéis usar cualquiera de las tres sin problema. Si os conformáis con un resultado rápido, las dos primeras son una buena opción y si queréis invertir algo más de tiempo usad la tercera.
Referencias
Enlaces
- Arduino IDE
- PIDLab web
- Arduino COM Plotter
- Métodos de sintonización en lazo abierto
- Cálculo manual de T1(28,3%) y T2(63,2%) [PDF] [Youtube]
- Diseño de sistemas de control. Sintonía de PIDs (UPV-EHU)
Libros y publicaciones
[1] Tore Hagglund. Process Control in Practice, De Gruyter, ISBN: 9783111104959
[2] Karl J. Astrom, Tore Hagglund. Control PID avanzado, Pearson, ISBN: 978-84-8322-511-0
[3] Daniel Chuck. Los sistemas de primer orden y los controladores PID, edición 2012. [Link] [Link2]
[4] J.G. Ziegler, N.B. Nichols. Optimum Settings For Automatic Controllers, 1942 edition, American Society of Mechanical Engineers. [Link]
[5] G.H. Cohen, G.A. Coon. Theoretical Consideration of Retarded Control, 1953 edition, American Society of Mechanical Engineers. [Link] [Link2]
[6] Daniel E. Rivera. Internal Model Control: A Comprehensive View, 1999 edition, College of Engineering and Applied Sciences. [Link]
[7] R. Vilanova, A. Visioli. PID Control in the Third Millennium. Chapter 5, The SIMC Method for smooth PID Controller Tuning, Springer. ISBN: 978-1-4471-2424-5.
[8] Guillermo J. Silva, Aniruddha Datta, S.P. Bhattacharyya. PID Controllers for Time-Delay Systems. Chapter 10, Analysis of Some PID Tunning Techniques. Birkhäuser. ISBN: 0-8176-4266-8
[9] Acedo Sánchez, José. Instrumentación y control avanzado de procesos, Diaz de Santos, ISBN: 978-84-7978-754-7.
[10] Morilla García, Fernando. ¿Qué quieres controlar? ¿Has probado con controladores PID?. Dpto. de Informática y Automática UNED. [Link]
[11] Aidan O’Dwyer. Handbook of PI and PID controller tuning rules, 3rd edition, Imperial College Press. ISBN: 978-1-84816-242-6