
Regresión no lineal – Accord.NET vs Math.NET Numerics
Recientemente he estado trabajando bastante con la librería Math.NET Numerics, y debo decir que me ha dejado muy buen sabor de boca. Es por ello que he decidido volver a plantear el problema de regresión no lineal, originalmente abordado en la entrada “Regresión lineal y no lineal – Excel vs NET”, para realizar una comparativa entre la ya conocida Accord y la reciente incorporación de Math.NET Numerics.
En esta ocasión iré directo al grano y os presentaré ambas implementaciones en VB.Net. Como recordatorio, el problema consiste en obtener, mediante regresión no lineal, los tres parámetros de la ecuación de Antoine a partir de unas temperaturas y presiones dadas.
Accord.NET
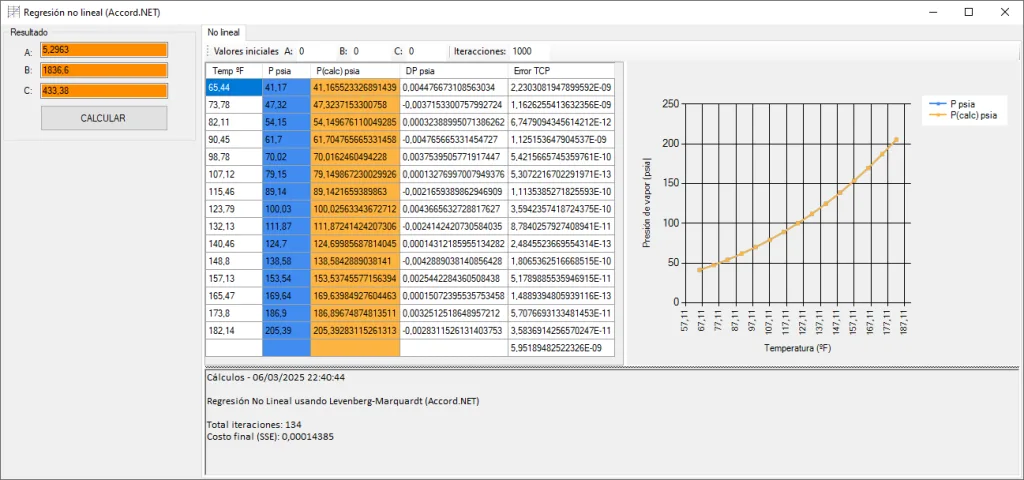
Los más observadores ya os habréis dado cuenta de que he actualizado la función. La vez anterior no me quede del todo satisfecho con el mínimo local que devolvía el algoritmo y he retocado la parte de las iteraciones y la tolerancia para mejorar esto. El resultado es que conseguimos los mismos valores que con la regresión lineal del artículo anterior, es decir, en esta ocasión el resultado roza la perfección incluso aunque no le indiquemos valores iniciales.
Public Sub CalcNoLineal_Accord()
Try
' --- 1. Preparar DataTable y DataGridView (DGV_API_NL) ---
Txt_Resul_NL.Text = ""
TXT_A.Text = ""
TXT_B.Text = ""
TXT_C.Text = ""
Dim dt As Date = Now
Txt_Resul_NL.Text = "Cálculos - " & dt.ToString("dd/MM/yyyy HH:mm:ss", Globalization.CultureInfo.InvariantCulture) & vbNewLine & vbNewLine
Txt_Resul_NL.Text &= "Regresión No Lineal usando Levenberg-Marquardt (Accord.NET)" & vbNewLine & vbNewLine
Dim dt_api_NL As New DataTable
dt_api_NL.Columns.Add("Temp ºF")
dt_api_NL.Columns.Add("P psia")
dt_api_NL.Columns.Add("P(calc) psia")
dt_api_NL.Columns.Add("DP psia")
dt_api_NL.Columns.Add("Error TCP")
' Llenar la tabla con 15 datos (índices 0 a 14)
For i As Integer = 0 To 14
dt_api_NL.Rows.Add(New String() {T(i).ToString(), P(i).ToString(), "0", "0", "0"})
Next
DGV_API_NL.DataSource = dt_api_NL
DGV_API_NL.AutoSizeColumnsMode = DataGridViewAutoSizeColumnsMode.AllCells
DGV_API_NL.AllowUserToOrderColumns = False
DGV_API_NL.RowHeadersVisible = False
DGV_API_NL.ColumnHeadersVisible = True
Application.DoEvents()
' --- 2. Extraer datos de la tabla en arrays ---
Dim rowCount As Integer = dt_api_NL.Rows.Count
Dim TData(rowCount - 1) As Double
Dim PData(rowCount - 1) As Double
For i As Integer = 0 To rowCount - 1
TData(i) = CDbl(dt_api_NL.Rows(i)("Temp ºF"))
PData(i) = CDbl(dt_api_NL.Rows(i)("P psia"))
Next
' --- 3. Transformar los datos: cada entrada es un vector unidimensional ---
Dim inputs As Double()() = TData.Select(Function(t) New Double() {t}).ToArray()
Dim output As Double() = PData
' --- 4. Configurar la regresión no lineal ---
' Modelo: P = 10^( A - B/(T + C) )
Dim nls As New NonlinearLeastSquares()
With nls
.NumberOfParameters = 3 ' A, B, C
' Valores iniciales (leídos de controles)
.StartValues = {CDbl(Txt_A_ini.Text), CDbl(Txt_B_ini.Text), CDbl(Txt_C_ini.Text)}
'
' Función del modelo: recibe los parámetros y un vector de entrada (T)
.Function = Function(par As Double(), inp As Double()) As Double
Return 10 ^ (par(0) - par(1) / (inp(0) + par(2)))
End Function
'
' Función del gradiente: se debe llenar el arreglo result con las derivadas parciales
.Gradient = Sub(par As Double(), inp As Double(), result() As Double)
Dim ln10 As Double = Math.Log(10)
Dim pred As Double = 10 ^ (par(0) - par(1) / (inp(0) + par(2)))
result(0) = ln10 * pred ' d/dA
result(1) = -ln10 * pred / (inp(0) + par(2)) ' d/dB
result(2) = (par(1) * ln10 * pred) / ((inp(0) + par(2)) ^ 2) ' d/dC
End Sub
End With
' --- 5. Configurar el algoritmo de optimización (Levenberg-Marquardt) ---
Dim algorithm As New LevenbergMarquardt()
With algorithm
.MaxIterations = 1 ' Iteraciones por bloque
.Tolerance = 0.000000000000001 ' Tolerancia para cambio en SSE -> 1e-15
End With
nls.Algorithm = algorithm
' --- 6. Ejecutar el ajuste con detención temprana ---
Dim totalMaxIter As Integer = CInt(Txt_iter.Text)
Dim totalIter As Integer = 0
Dim tolerance As Double = 0.000000000000001 '1e-15
' Función local para calcular el SSE (suma de cuadrados de errores)
Dim ComputeSSE As Func(Of Double(), Double) =
Function(coeffs As Double()) As Double
Dim sumSq As Double = 0
For j As Integer = 0 To inputs.Length - 1
Dim pred As Double = 10 ^ (coeffs(0) - coeffs(1) / (inputs(j)(0) + coeffs(2)))
Dim resid As Double = pred - output(j)
sumSq += resid * resid
Next
Return sumSq
End Function
Dim currentSolution() As Double = nls.StartValues
Dim previousCost As Double = ComputeSSE(currentSolution)
Dim currentCost As Double = previousCost
Do
nls.StartValues = currentSolution
Dim regression As NonlinearRegression = nls.Learn(inputs, output)
currentSolution = regression.Coefficients
totalIter += 1
currentCost = ComputeSSE(currentSolution)
If Math.Abs(previousCost - currentCost) < tolerance Then Exit Do
previousCost = currentCost
Loop While totalIter < totalMaxIter
' --- 7. Mostrar los parámetros ajustados ---
TXT_A.Text = currentSolution(0).ToString("G5")
TXT_B.Text = currentSolution(1).ToString("G5")
TXT_C.Text = currentSolution(2).ToString("G5")
A = currentSolution(0)
B = currentSolution(1)
C = currentSolution(2)
APIcalc()
' --- 8. Graficar los resultados ---
Chart2.Series.Clear()
Chart2.Legends.Clear()
Chart2.Legends.Add("")
Chart2.Titles.Clear()
Chart2.Titles.Add("")
Chart2.Titles(0).Font = New Font("Microsoft Sans Serif", 12, FontStyle.Bold)
For i As Integer = 1 To 2
Chart2.Series.Add(dt_api_NL.Columns(i).ColumnName)
With Chart2.Series(Chart2.Series.Count - 1)
.MarkerStyle = DataVisualization.Charting.MarkerStyle.Square
.IsVisibleInLegend = True
.ChartType = DataVisualization.Charting.SeriesChartType.Line
.BorderWidth = 2
.ToolTip = "#SERIESNAME | T: #VALX{f2} P: #VALY{f2}"
For j As Integer = 0 To rowCount - 1
Dim Tval As Double = CDbl(dt_api_NL.Rows(j)("Temp ºF"))
Dim Pval As Double = CDbl(dt_api_NL.Rows(j)(i))
.Points.AddXY(Tval, Pval)
Next
End With
Next
Chart2.ChartAreas(0).AxisX.Title = "Temperatura (ºF)"
Chart2.ChartAreas(0).AxisY.Title = "Presión de vapor (psia)"
Chart2.ChartAreas(0).RecalculateAxesScale()
Txt_Resul_NL.Text &= "Total iteraciones: " & totalIter.ToString() & vbNewLine
Txt_Resul_NL.Text &= "Costo final (SSE): " & currentCost.ToString("G5") & vbNewLine
Catch ex As Exception
MsgBox(ex.ToString())
End Try
End Sub
Math.NET Numerics
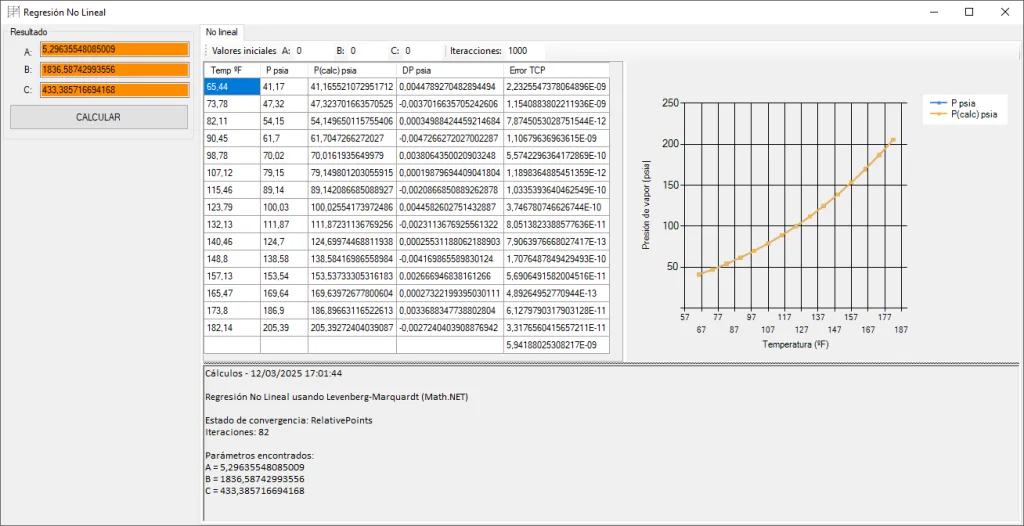
Esta implementación es completamente nueva pero para que os hagáis una idea, me ha costado más modificar la función de Accord para que mostrara bien las iteraciones que crear esta función de cero. Creo que sin duda, eso dice mucho de la facilidad de uso de esta librería.
Public Sub CalcNoLineal_MathNet()
Try
' ---------------------------------------------------
' 1. PREPARAR DataTable Y DataGridView (DGV_API_NL)
' ---------------------------------------------------
Txt_Resul_NL.Text = ""
TXT_A.Text = ""
TXT_B.Text = ""
TXT_C.Text = ""
Dim dt As Date = Now
Txt_Resul_NL.Text = "Cálculos - " & dt.ToString("dd/MM/yyyy HH:mm:ss", CultureInfo.InvariantCulture) & vbNewLine & vbNewLine
Txt_Resul_NL.Text &= "Regresión No Lineal usando Levenberg-Marquardt (Math.NET)" & vbNewLine & vbNewLine
' Creamos la tabla para mostrar Temp, P, etc.
Dim dt_api_NL As New DataTable
dt_api_NL.Columns.Add("Temp ºF")
dt_api_NL.Columns.Add("P psia")
dt_api_NL.Columns.Add("P(calc) psia")
dt_api_NL.Columns.Add("DP psia")
dt_api_NL.Columns.Add("Error TCP")
' Llenamos la tabla con los 15 datos T(i), P(i)
For i = 0 To 14
dt_api_NL.Rows.Add(New String() {
T(i).ToString(),
P(i).ToString(),
"0", "0", "0"
})
Next i
' Asignamos al DGV
DGV_API_NL.DataSource = dt_api_NL
DGV_API_NL.AutoSizeColumnsMode = DataGridViewAutoSizeColumnsMode.AllCells
DGV_API_NL.AllowUserToOrderColumns = False
DGV_API_NL.RowHeadersVisible = False
DGV_API_NL.ColumnHeadersVisible = True
Application.DoEvents()
' ---------------------------------------------------
' 2. EXTRAER DATOS DE LA TABLA => Vectores TDataVector, PDataVector
' ---------------------------------------------------
Dim rowCount As Integer = dt_api_NL.Rows.Count
Dim TData As Double() = New Double(rowCount - 1) {}
Dim PData As Double() = New Double(rowCount - 1) {}
For i = 0 To rowCount - 1
TData(i) = CDbl(dt_api_NL.Rows(i)("Temp ºF"))
PData(i) = CDbl(dt_api_NL.Rows(i)("P psia"))
Next
' Creamos vectores Math.NET
Dim TDataVector As Vector(Of Double) = Vector(Of Double).Build.DenseOfArray(TData)
Dim PDataVector As Vector(Of Double) = Vector(Of Double).Build.DenseOfArray(PData)
' ---------------------------------------------------
' 3. DEFINIR FUNCION MODELO + JACOBIANO
'
' Modelo: P = 10^( A - B/(T + C) )
' => firma: Func(Of Vector(Of Double), Double, Double)
' => jacobiano: Func(Of Vector(Of Double), Double, Vector(Of Double))
' ---------------------------------------------------
Dim modelFunction As Func(Of Vector(Of Double), Double, Double) =
Function(par, x)
Dim A_ As Double = par(0)
Dim B_ As Double = par(1)
Dim C_ As Double = par(2)
Dim Q = A_ - (B_ / (x + C_))
Return 10.0 ^ Q
End Function
Dim jacobianFunction As Func(Of Vector(Of Double), Double, Vector(Of Double)) =
Function(par, x)
Dim A_ As Double = par(0)
Dim B_ As Double = par(1)
Dim C_ As Double = par(2)
Dim ln10 As Double = Math.Log(10.0)
Dim Q = A_ - (B_ / (x + C_))
Dim F = 10.0 ^ Q
Dim dFdA = ln10 * F
Dim dFdB = -ln10 * F / (x + C_)
Dim dFdC = ln10 * F * B_ / ((x + C_) ^ 2)
Return Vector(Of Double).Build.DenseOfArray({dFdA, dFdB, dFdC})
End Function
' ---------------------------------------------------
' 4. CREAR IObjectiveModel CON NonlinearModel
' ---------------------------------------------------
Dim objective As IObjectiveModel =
ObjectiveFunction.NonlinearModel(
modelFunction,
jacobianFunction,
TDataVector,
PDataVector
)
' ---------------------------------------------------
' 5. LEER ESTIMACION INICIAL Y AJUSTAR
' ---------------------------------------------------
Dim A_ini As Double = CDbl(Txt_A_ini.Text)
Dim B_ini As Double = CDbl(Txt_B_ini.Text)
Dim C_ini As Double = CDbl(Txt_C_ini.Text)
Dim initialGuess = Vector(Of Double).Build.DenseOfArray(New Double() {A_ini, B_ini, C_ini})
Dim lm As New LevenbergMarquardtMinimizer()
lm.MaximumIterations = CInt(Txt_iter.Text)
Dim result = lm.FindMinimum(objective, initialGuess)
' ---------------------------------------------------
' 6. Extraer parámetros ajustados => {A_Opt, B_Opt, C_Opt}
' ---------------------------------------------------
Dim pOptim = result.MinimizingPoint
Dim A_Opt = pOptim(0)
Dim B_Opt = pOptim(1)
Dim C_Opt = pOptim(2)
' Actualizar TextBoxes
TXT_A.Text = A_Opt.ToString()
TXT_B.Text = B_Opt.ToString()
TXT_C.Text = C_Opt.ToString()
' Mostrar info de convergencia en Txt_Resul_NL
Txt_Resul_NL.Text &= $"Estado de convergencia: {result.ReasonForExit}" & vbNewLine
Txt_Resul_NL.Text &= $"Iteraciones: {result.Iterations}" & vbNewLine & vbNewLine
Txt_Resul_NL.Text &= $"Parámetros encontrados:" & vbNewLine
Txt_Resul_NL.Text &= $"A = {A_Opt}" & vbNewLine
Txt_Resul_NL.Text &= $"B = {B_Opt}" & vbNewLine
Txt_Resul_NL.Text &= $"C = {C_Opt}" & vbNewLine & vbNewLine
' ---------------------------------------------------
' 7. CALCULAR P(calc) y actualizar la tabla
' ---------------------------------------------------
A = A_Opt
B = B_Opt
C = C_Opt
APIcalc()
' ---------------------------------------------------
' 8. GRAFICAR RESULTADOS EN Chart2
' Se grafican las columnas "P psia" y "P(calc) psia"
' ---------------------------------------------------
Chart2.Series.Clear()
Chart2.Legends.Clear()
Chart2.Legends.Add("")
Chart2.Titles.Clear()
Chart2.Titles.Add("")
Chart2.Titles(0).Font = New Font("Microsoft Sans Serif", 12, FontStyle.Bold)
' ColIndex=1 => "P psia"
' ColIndex=2 => "P(calc) psia"
For colIndex As Integer = 1 To 2
Chart2.Series.Add(dt_api_NL.Columns(colIndex).ColumnName)
With Chart2.Series(Chart2.Series.Count - 1)
.MarkerStyle = DataVisualization.Charting.MarkerStyle.Square
.IsVisibleInLegend = True
.ChartType = DataVisualization.Charting.SeriesChartType.Line
.BorderWidth = 2
.ToolTip = "#SERIESNAME | T: #VALX{f2} P: #VALY{f2}"
For j = 0 To rowCount - 1
Dim Tval = CDbl(dt_api_NL.Rows(j)("Temp ºF"))
Dim Pval = CDbl(dt_api_NL.Rows(j)(colIndex))
.Points.AddXY(Tval, Pval)
Next
End With
Next
' Ajustes de ejes
Chart2.ChartAreas(0).AxisX.Title = "Temperatura (ºF)"
Chart2.ChartAreas(0).AxisY.Title = "Presión de vapor (psia)"
Chart2.ChartAreas(0).AxisX.LabelStyle.Format = "#"
Chart2.ChartAreas(0).AxisY.LabelStyle.Format = "#"
' Recalcular ejes
Chart2.ChartAreas(0).RecalculateAxesScale()
Catch ex As Exception
MsgBox(ex.ToString)
End Try
End Sub
Comparativa
Ambos códigos utilizan el algoritmo de optimización Levenberg-Marquardt, una tolerancia de error de 1e-6 y tienen fijado un máximo de iteraciones de 1000.
| Iteraciones con A=2 B=1500 C=273 | Iteraciones con A=100 B=100 C=100 | Iteraciones con A=0 B=0 C=0 | |
| Accord.NET | 45 | No soluciona | 149 |
| Math.NET Numerics | 47 | 812 | 82 |
Conclusiones
Las dos librerías han logrado encontrar el mejor resultado posible casi sin esfuerzo, ahora bien, Math.NET Numerics gana por goleada en facilidad de uso e implementación. Excepto usando valores negativos en los que ambos algoritmos han fallado, el algoritmo de minimización de Math.NET ha resultado mucho más óptimo. Otro punto en contra de Accord.Net es que parece que su desarrollo se ha estancado, siendo su último lanzamiento en 2017 cuando Math.NET Numerics sigue en continuo desarrollo en 2025. Esto no quiere decir que Accord.NET sea una librería a desechar, ya que, incluso tiene más funcionalidades que Math.NET Numerics, aunque en mi humilde opinión la discontinuidad y la falta de comunidad siempre te lastran.
Enlaces
- Accord.NET [Github] [Doc]
- Math.NET Numerics [Github] [Doc]
- Fuentes VS2019 [garikoitz.info]
- Ecuación de Antoine [Wikipedia]
- Algoritmo Levenberg-Marquardt [Wikipedia]
- Regresión lineal y no lineal – Excel vs NET [garikoitz.info]