Sintonizar PID con Arduino – Balancín simple

Introducción

Aquí tenéis la segunda entrega sobre sintonización PID. En la primera entrega vimos un control de temperatura y en esta veremos un control de posición de un balancín simple.

Sistema empleado

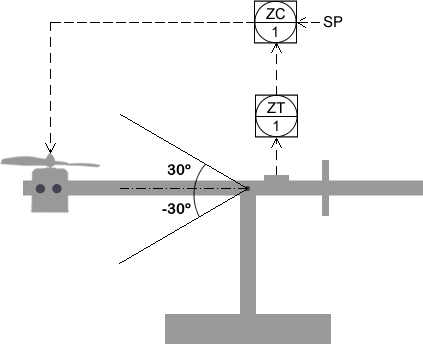
Se trata de un balancín simple con inclinación en un solo eje, que consta de un motor de corriente continua con hélice y un giroscopio / acelerómetro que hará de sensor para calcular la inclinación.

La maqueta está hecha con caña de bambú y madera y consta de solo 2 componentes principales, el motor de corriente continua y el acelerómetro. El motor de corriente continua es de 5V pero necesita una fuente de alimentación externa ya que consume entre 750mA y 1,8A.

El objetivo es mediante un controlador PID situar el balancín en el ángulo de inclinación deseado. Nos movemos en un rango de entre 30 y -30º.

Componentes

• Arduino UNO R3
• Sensor acelerador + giroscopio MPU6050 (GY-521)
• Motor CC (L9110 Keyes)
• Microinterruptor*
• Potenciómetro de 10K**
• Una resistencia de 220 ohm
• Una fuente externa de 5 voltios
• Cables dupont para el conexionado
• Una mini protoboard

* El microinterruptor nos sirve para conmutar entre Automático y Manual.

** En manual el potenciómetro altera la OP. En automático altera el SP.

El coste de los componentes es de aproximadamente 30-40€ sin contar la fuente de alimentación externa.

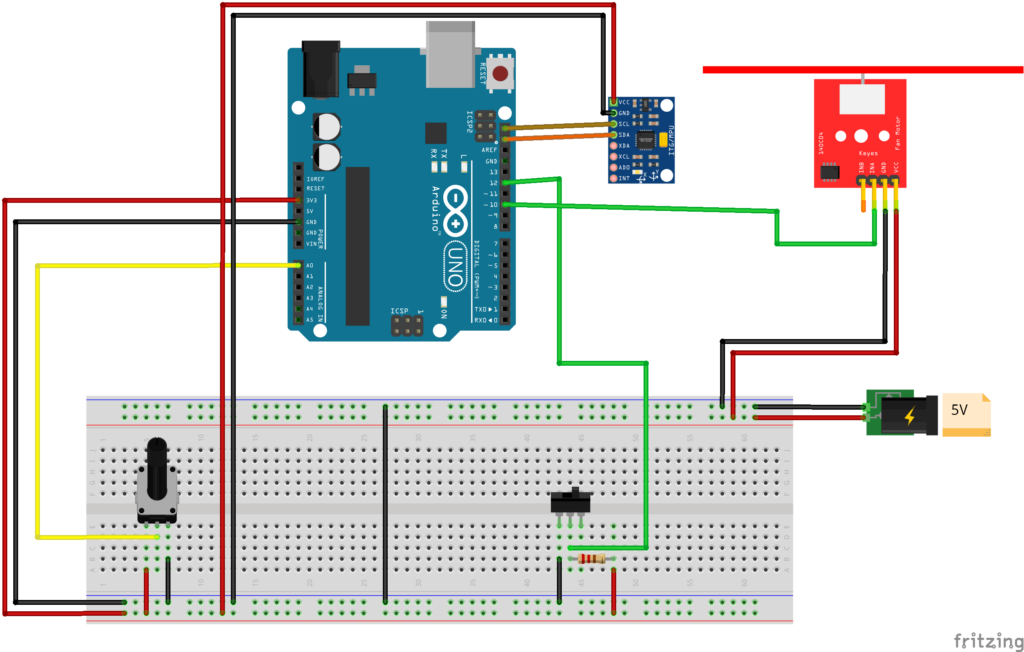
Esquema de conexiones

Código de Arduino

Notas:

• Para evitar problemas y errores se han convertido a porcentaje todas las variables.
• Para la conversión de rangos con decimales se ha implementado la función MAPF, ya que la función MAP nativa de Arduino devuelve simplemente un long integer.

/***************************************************************
* Desarrollado por Garikoitz Martínez [garikoitz.info] [06/2020]
* https://garikoitz.info/blog/?p=890
***************************************************************/
/***************************************************************
* Librerías
***************************************************************/
#include "I2Cdev.h"
#include "MPU6050.h"
#include <Wire.h>
#include <PID_v1.h>
/***************************************************************
* Variables
***************************************************************/
  //Hélice
  const int INA = 10; //Motor Forward
  const int INB = 11; //Motor Reverse
  const int Interruptor = 12;
  const int pot = 0;                                                                                //Potenciómetro en pin A0
  unsigned long previousMillis = 0;
  int Ts = 100; //Sample time 100ms
  //Giroscópio
  const int mpuAddress = 0x68;  //Puede ser 0x68 o 0x69
  MPU6050 mpu(mpuAddress);
  //Offsets de calibración
  #define MPU6050_ACCEL_OFFSET_X -2936
  #define MPU6050_ACCEL_OFFSET_Y 1412
  #define MPU6050_ACCEL_OFFSET_Z 962
  #define MPU6050_GYRO_OFFSET_X  58
  #define MPU6050_GYRO_OFFSET_Y  85
  #define MPU6050_GYRO_OFFSET_Z  15
  int ax, ay, az;
  int gx, gy, gz;
  float ang_x, ang_y;
  float ang_x_prev, ang_y_prev;
  long tiempo_prev;
  float dt;
  //Control PID
  boolean modo = false; //false=auto true=manual
  float tmp = 0;
  float tmp_ant = 0;
  float OP = 0;
  double SetpointP, InputP, OutputP;
  double Kp=6, Ki=3, Kd=2;
  PID myPID(&InputP, &OutputP, &SetpointP, Kp, Ki, Kd,P_ON_E, DIRECT);    //PI-D
  //PID myPID(&InputP, &OutputP, &SetpointP, Kp, Ki, Kd,P_ON_M, DIRECT);  //I-PD
/***************************************************************
* SETUP
***************************************************************/
void setup() 
{ 
  //Hélice
  pinMode(INA,OUTPUT); 
  pinMode(INB,OUTPUT); 
  pinMode(Interruptor, INPUT);
  //PID 
  myPID.SetSampleTime(50);        //PID calcula cada 50ms. Por defecto es cada 100ms.
  myPID.SetOutputLimits(0, 100);
  myPID.SetMode(MANUAL);
  //Giroscópio
  mpu.initialize();
  //Calibración
  mpu.setXAccelOffset(MPU6050_ACCEL_OFFSET_X);
  mpu.setYAccelOffset(MPU6050_ACCEL_OFFSET_Y);
  mpu.setZAccelOffset(MPU6050_ACCEL_OFFSET_Z);
  mpu.setXGyroOffset(MPU6050_GYRO_OFFSET_X);
  mpu.setYGyroOffset(MPU6050_GYRO_OFFSET_Y);
  mpu.setZGyroOffset(MPU6050_GYRO_OFFSET_Z);
  Serial.println(mpu.testConnection() ? F("IMU iniciado correctamente") : F("Error al iniciar IMU"));
  Serial.begin(9600);
}
/***************************************************************
* BUCLE PRINCIPAL
***************************************************************/
void loop() 
{
  if (millis() - previousMillis > Ts) 
  {
    previousMillis = millis();
    if (digitalRead(12) == HIGH){
      modo=true;//Manual
      myPID.SetMode(MANUAL);
    }else{
      digitalWrite(INB ,LOW);
      analogWrite(INA,OP);   //Forward
      modo=false;//Automático
      myPID.SetMode(AUTOMATIC);
    }
    mpu.getAcceleration(&ax, &ay, &az);
    mpu.getRotation(&gx, &gy, &gz);
    //Calcular los ángulos con acelerometro
    double accel_ang_x=atan(ay/sqrt(pow(ax,2) + pow(az,2)))*(180.0/3.14);
    double accel_ang_y=atan(-ax/sqrt(pow(ay,2) + pow(az,2)))*(180.0/3.14);
    dt = (millis()-tiempo_prev)/1000.0;
    tiempo_prev=millis();
    //Ángulo de rotación y filtro complementario 
    ang_x = 0.98*(ang_x_prev+(gx/131)*dt) + 0.02*accel_ang_x;
    ang_x_prev=ang_x;
    //
    /***************************************************************
    * Modo MANUAL - Potenciómetro ---> PWM Motor CC
    ***************************************************************/
    if (modo==true){
      SetpointP=0;
      //Leo el sensor
      InputP = mapf(ang_x, -30, 30, 0, 100);          //Filtro complementario
      //Leo el potenciómetro
      //Evitar saltos del 0.85% al leer el potenciómetro
      tmp = analogRead(pot);
      tmp = mapf(tmp, 0, 1023, 0, 100);
      if(abs(tmp-tmp_ant)>0.85){
        OP = tmp;
      }
      tmp_ant=OP;
      digitalWrite(INB ,LOW);
      analogWrite(INA,OP/0.392156);   //FORWARD 0-100 a 0-255 para PWM
      /***************************************************************
      * DEBUG PUERTO SERIE (Para Arduino COM Plotter)
      ***************************************************************/
      Serial.print("#");             //Char inicio
      Serial.print(SetpointP,0);     //SP
      Serial.write(" ");             //Char separador
      Serial.print(InputP,3);        //PV
      Serial.write(" ");             //Char separador
      Serial.print(OP,0);            //OP
      Serial.println();
    }
    /***************************************************************
    * Modo AUTOMÁTICO - PID
    ***************************************************************/
    if (modo==false){
      tmp = analogRead(pot);
      tmp = mapf(tmp, 0, 1023, 0, 100);
      //Evitar saltos del 0.85% al leer el potenciómetro
      if(abs(tmp-tmp_ant)>0.85){
        SetpointP = tmp;
      }
      tmp_ant=SetpointP;
      InputP = mapf(ang_x, -30, 30, 0, 100);
      myPID.Compute();
      digitalWrite(INB ,LOW);
      analogWrite(INA,OutputP/0.392156); //FORWARD 0-100 a 0-255 para PWM
      /***************************************************************
      * DEBUG PUERTO SERIE (Para Arduino COM Plotter)
      ***************************************************************/
      Serial.print("#");                //Char inicio
      Serial.print(SetpointP,0);        //SP
      Serial.write(" ");                //Char separador
      Serial.print(InputP,3);           //PV
      Serial.write(" ");                //Char separador
      Serial.print(OutputP,0);          //OP
      Serial.println();
    }
  }
}
/***************************************************************
* FUNCIONES
***************************************************************/
//Función MAP adaptada a punto flotante.
double mapf(double val, double in_min, double in_max, double out_min, double out_max) {
    return (val - in_min) * (out_max - out_min) / (in_max - in_min) + out_min;
}

Identificación del sistema

Adecuando la señal del sensor

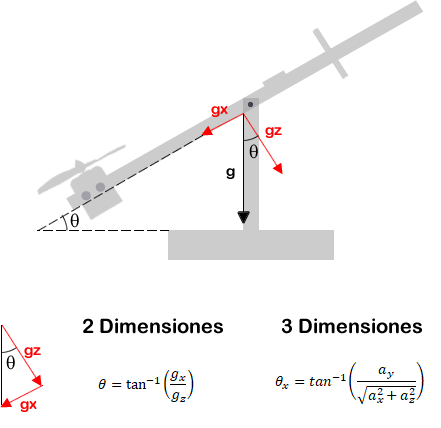
Del sensor recibimos 6 medidas, 3 aceleraciones y 3 velocidades angulares. Nosotros nos centraremos en las aceleraciones y en concreto en el ángulo theta del eje X. No me explayo más ya que este sensor da para una entrada del blog completa, os dejo en referencias unos artículos para que juzguéis vosotros mismos e indaguéis todas las posibilidades.

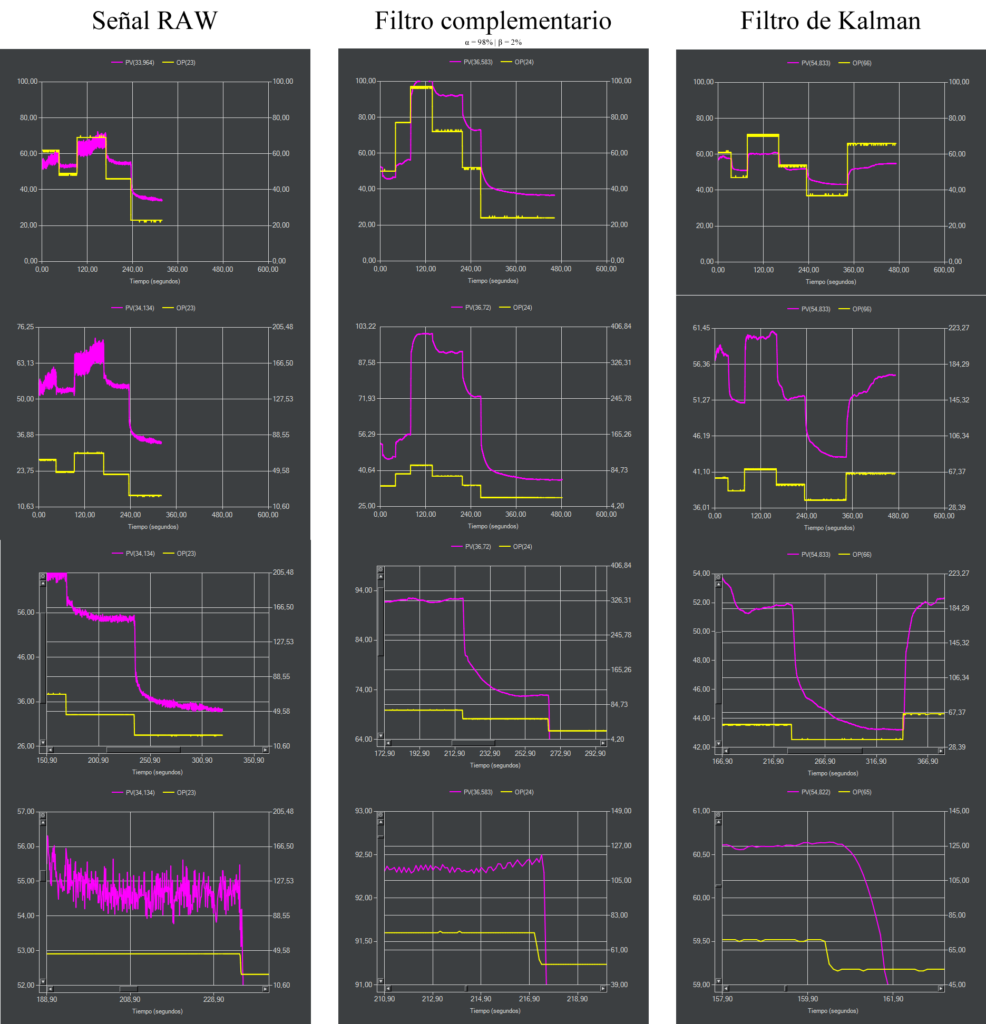
Las medidas resultantes del sensor son muy oscilantes y además debemos tener en cuenta el «drift» generado al integrar la velocidad angular con respecto del tiempo para hallar el ángulo deseado. La forma más sencilla de minimizar el drift es con un filtro complementario y la más elegante con un filtro de Kalman. El filtro complementario combina el ángulo calculado por el giroscopio con el ángulo calculado por el acelerómetro pudiendo dar más peso a uno o a otro dependiendo de nuestras necesidades. El filtro de Kalman es mucho más complejo pero a cambio el resultado es bastante mejor. En la imagen inferior vemos que ambos filtros hacen bien su trabajo pero que el filtro de Kalman está afectando a la respuesta del sistema por lo que habría que retocar los parámetros hasta encontrar los idóneos.

Hay que tener cierta precaución al utilizar filtros de cualquier tipo si lo que te planteas es hacer control con la señal filtrada. El filtro nos da una señal «limpia» pero a cambio el tiempo de respuesta es alterado. En resumen, cada caso requiere una reflexión que afectará a la sintonía de control.

Por sencillez implementaré un filtro complementario con la ecuación 1 y con los parámetros α=0.98 y β=0.02.

\begin{align}
& X = \alpha \left ( \left (X-1  \right )+\omega_{giroscopio} \ast dt  \right )+\beta\left ( \measuredangle \hspace{0.1cm} acelerometro \right )\\
& \alpha +\beta =1
\end{align}

Recopilación de datos en lazo abierto

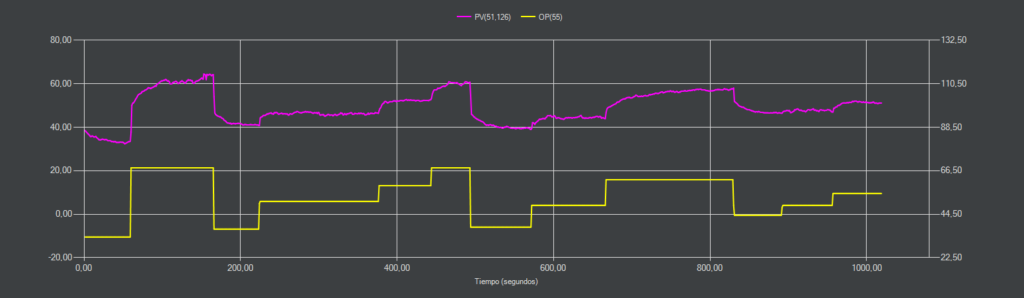
Con el interruptor en modo manual realizamos una serie de escalones para ver como reacciona el sensor con la ayuda de ACP.

Introduciendo los datos en ACP de un escalón representativo obtenemos las constantes del sistema que nos ayudarán a simular y a ajustar nuestro controlador.

Facilidad de control

El cociente entre T0 y Tp nos sugiere la facilidad de control de un sistema. En este caso estamos en la zona fácil ya que 1/1,5=0,66.

Ajuste y simulación en lazo cerrado

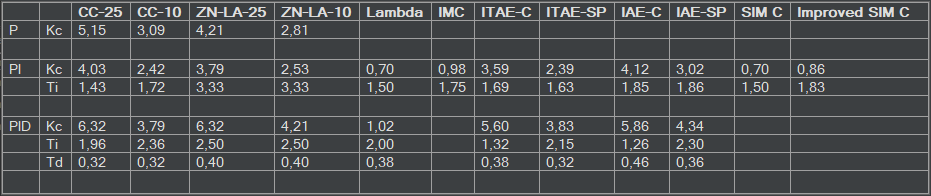
En la siguiente tabla tenemos las sintonías calculadas por ACP. ACP nos da Ti y Td pero la librería de arduino utiliza Ki y Kd por lo que hay que realizar la siguiente conversión:

\begin{align}
& K_{i}=\frac{K_{c}}{T_{i}} \hspace{0.2cm};\hspace{0.2cm} K_{d}={K_{c}}\times {T_{d}}
\end{align}

Resultados

A continuación veamos la respuesta de unas cuantas sintonías. El tiempo de muestreo es de 100ms.

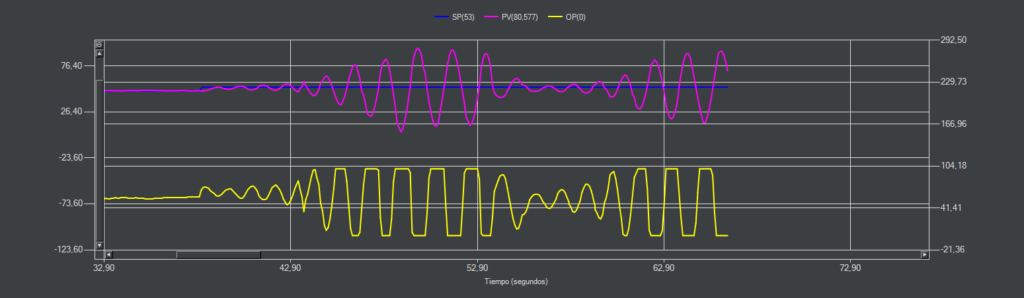
CC-25 (PI)

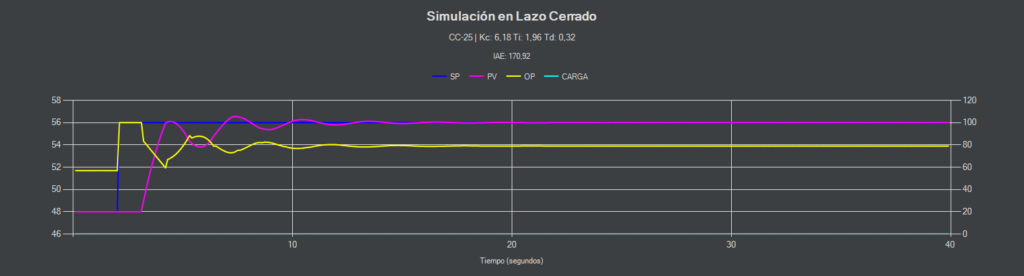
Como se aprecia en la imagen, un pequeño cambio en el punto de consigna hace que entre en oscilación continua. Posiblemente en esta maqueta, un sobre pasamiento del 25% con una estrategia PI no sea adecuado.

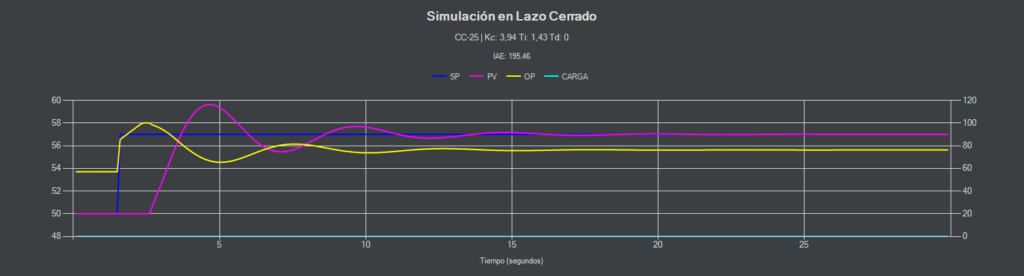
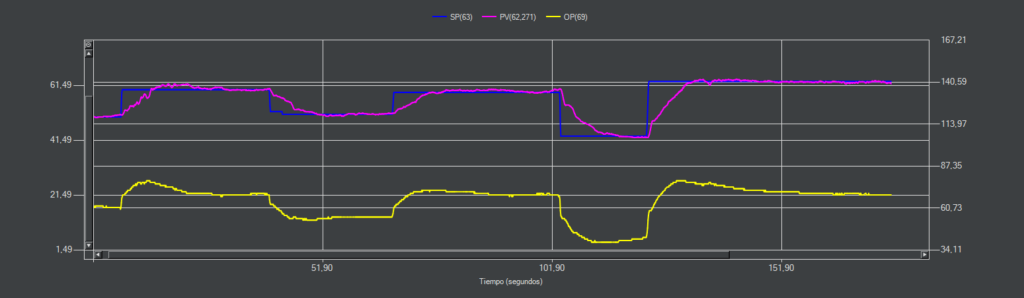
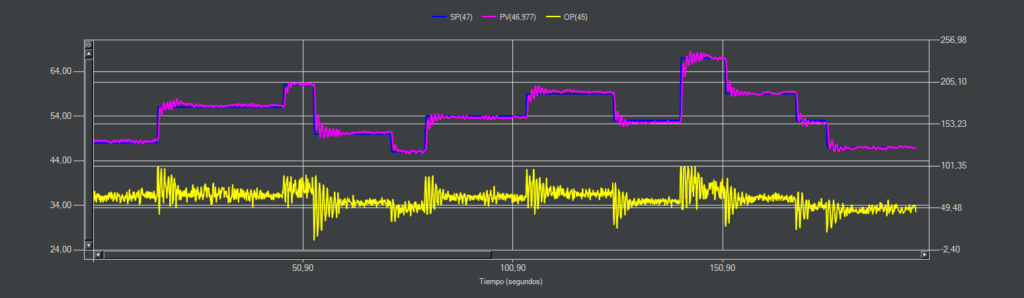
CC-25 (PI-D)

Al incluir el término derivativo ganamos en estabilidad. Ya no entra en oscilación continua aunque variemos el punto de consigna >10%.

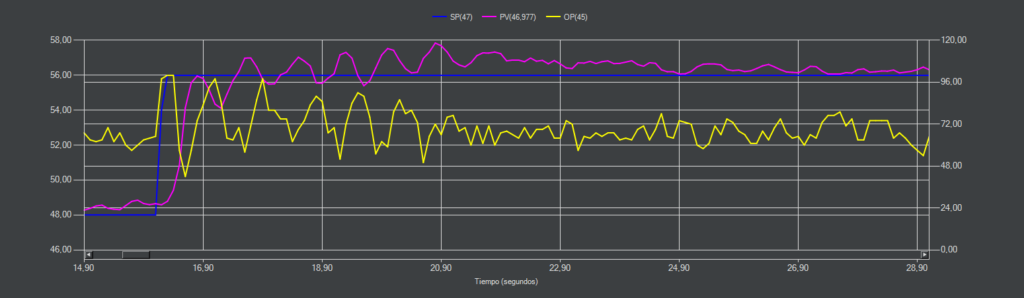
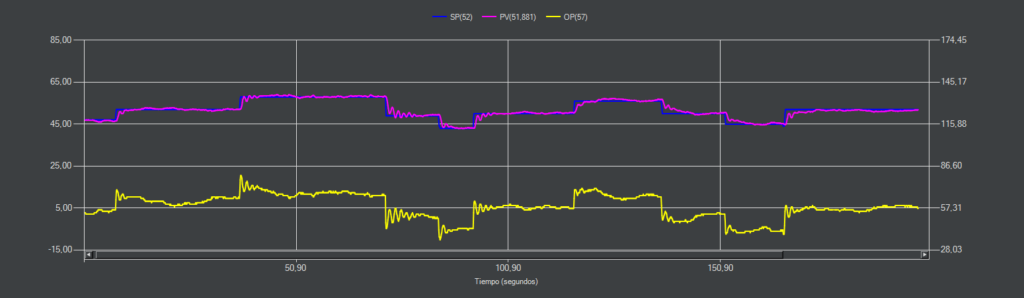
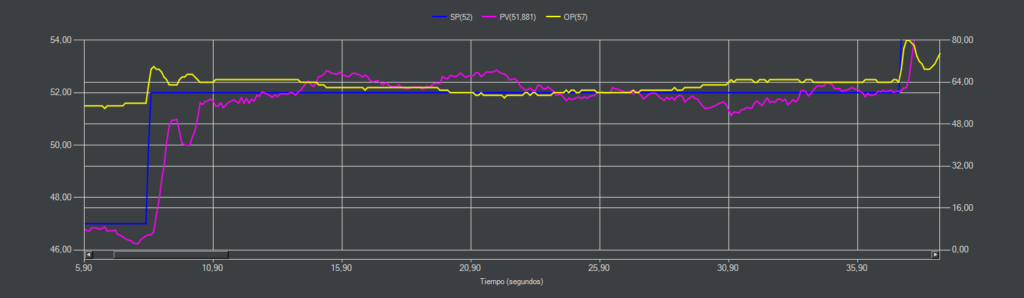
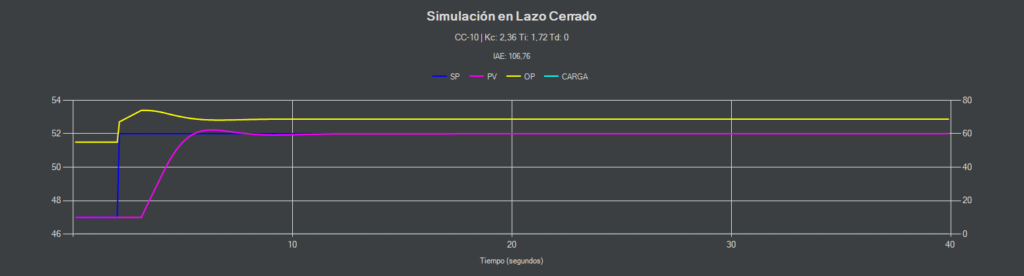
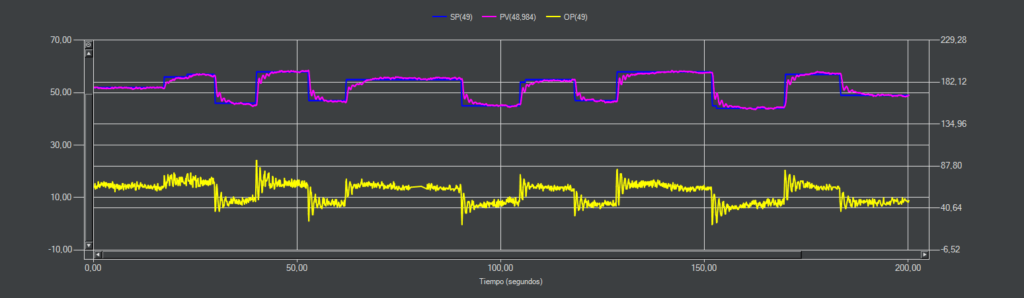
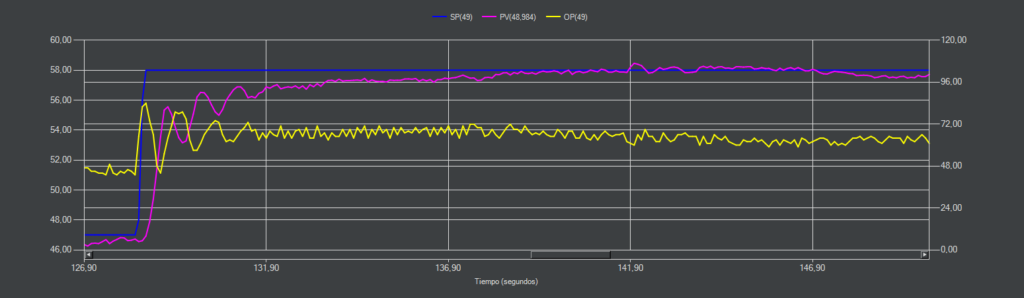
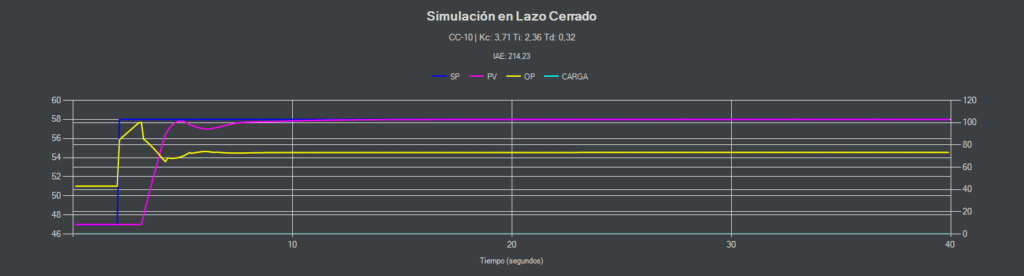
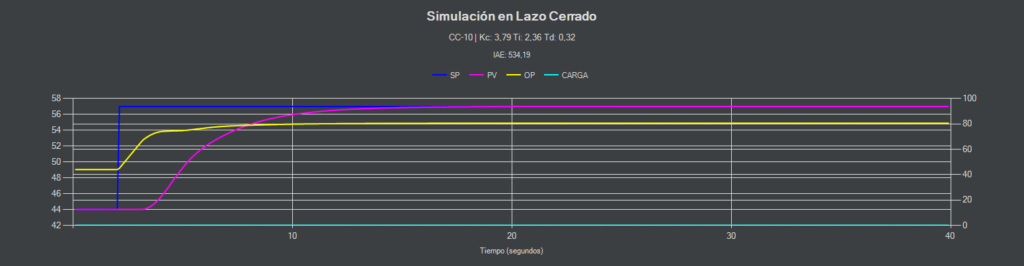
CC-10 (PI)

En esta ocasión con un sobrepasamiento del 10% la estrategia PI consigue mantenerse estable aunque la respuesta no es igual a la simulación.

CC-10 (PI-D)

De nuevo al incorporar el término derivativo se gana en estabilidad.

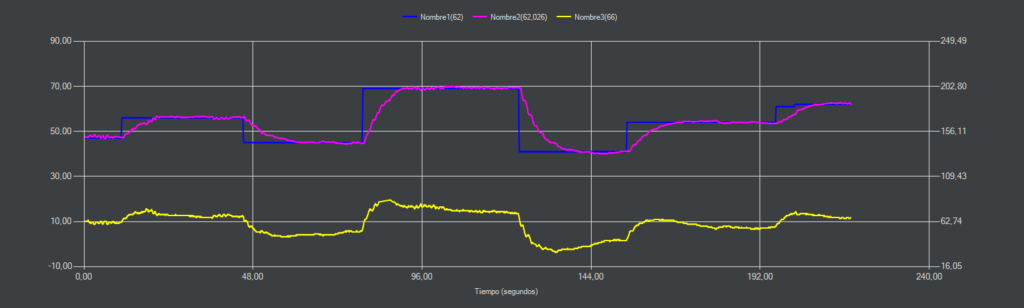
CC-10 (I-P)

Al utilizar un algoritmo I-P la respuesta del sistema se vuelve similar a una sintonía lambda o cualquier otra que utilice el parámetro «Tf». Esto es debido a que el algoritmo utiliza la PV en lugar del error en la constante proporcional suavizando la respuesta considerablemente.

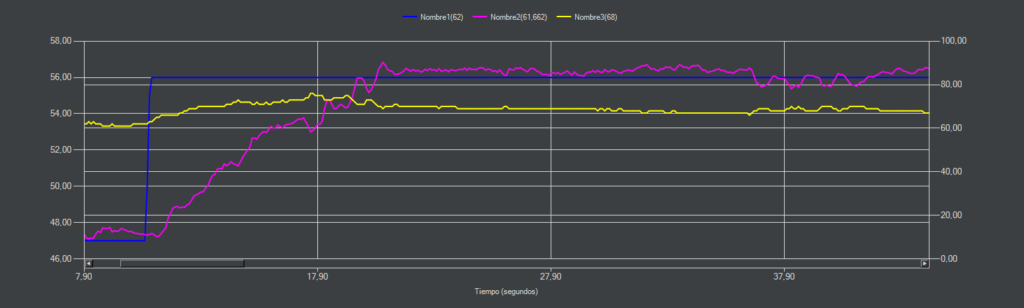
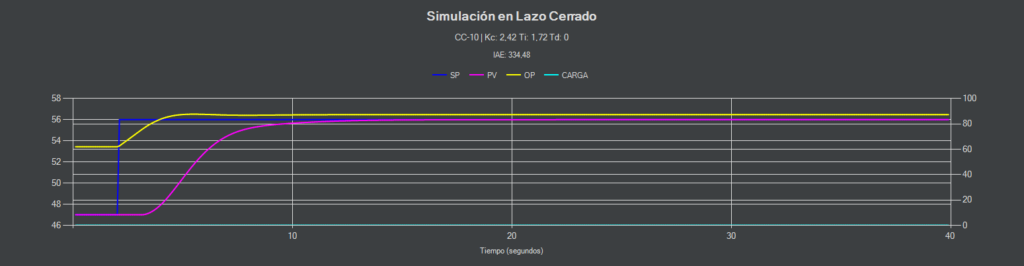
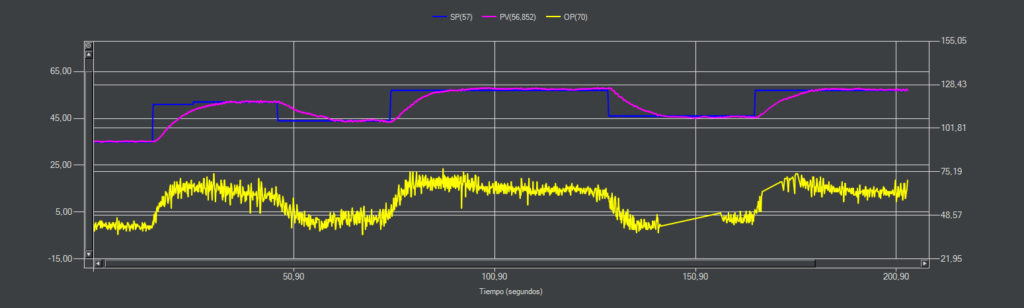
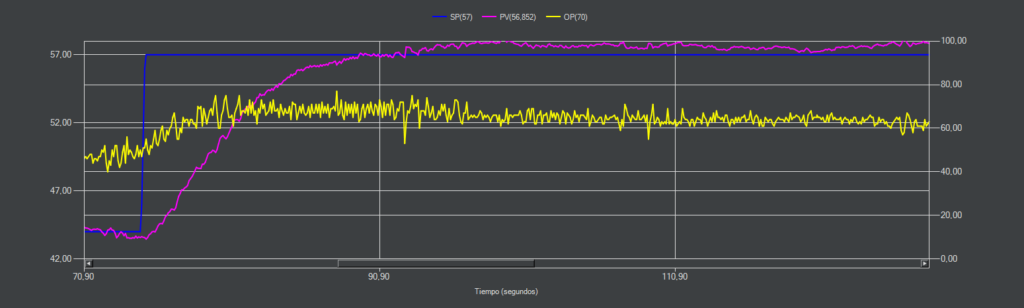
CC-10 (I-PD)

La respuesta es similar a la respuesta I-P pero al incluir el término derivativo, la salida se ha vuelto más oscilante.

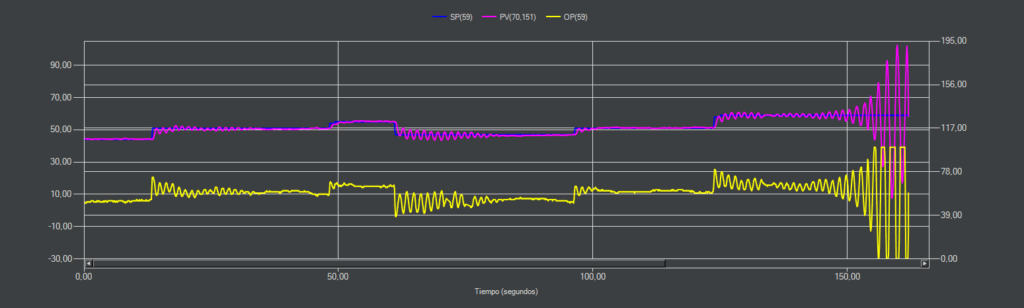
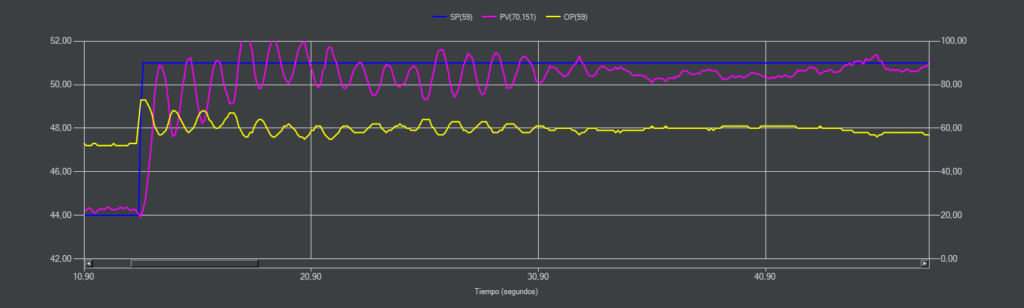
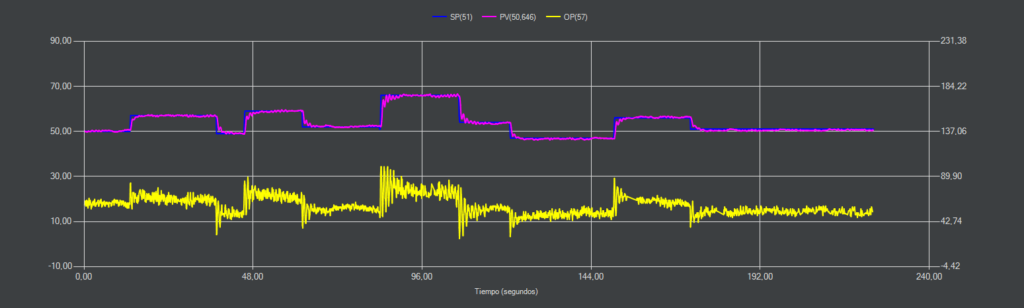
IAE-SP (PI)

Inicialmente aunque con más oscilaciones de las esperadas el control se mantiene estable, pero finalmente entra en oscilación continua tras una perturbación no medida.

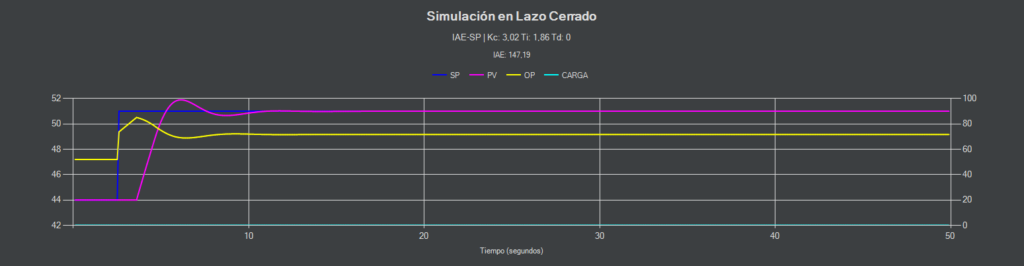
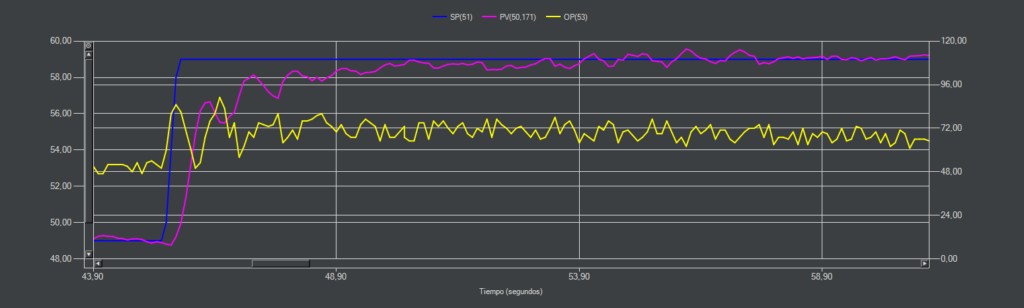
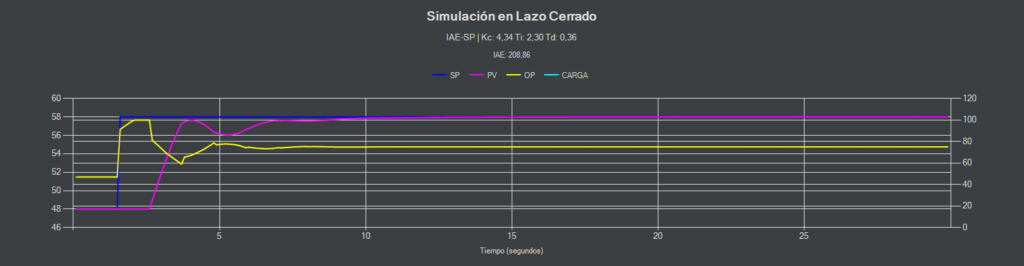
IAE-SP (PI-D)

El término derivativo da estabilidad incluso con cambios en el punto de consigna del 15%.

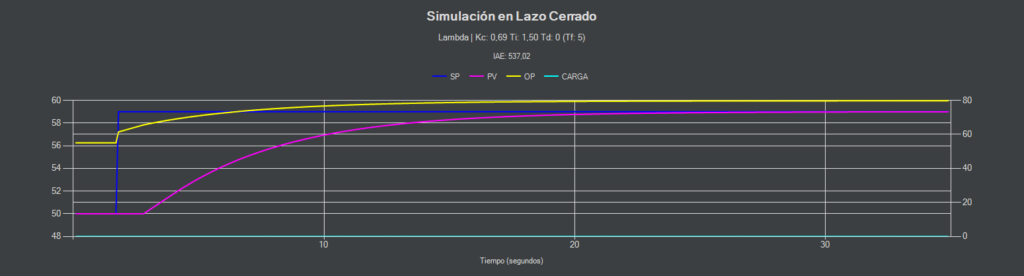
LAMBDA (PI)

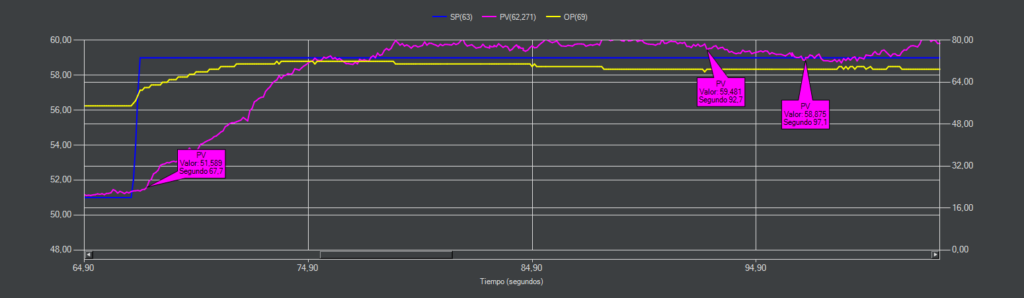
Con este método podemos ajustar mediante el parámetro Tf cuando queremos que la PV se iguale al SP. En este caso se ha utilizado un Tf = 5 por lo que la PV igualará al SP en 5 unidades de tiempo.

Haciendo un cálculo rápido tenemos que la PV y el SP se deberían igualar en el segundo 5×5+67,7 = 92,7. Como vemos, en la respuesta real hay un ligero sobrepasamiento inicial igualándose unos segundos más tarde, aunque dado que existe ruido en la PV se puede considerar se asemeja bastante con la simulación.

Conclusiones

Maqueta sencilla y control relativamente sencillo. Una vez identificado, todo depende de la respuesta que estemos buscando. Si buscamos una respuesta rápida nos decantaremos por métodos clásicos o métodos que busquen minimizar el índice de error. Si lo que buscamos es una respuesta suave podemos decantarnos por cualquier método afectado por el parámetro «Tf» o usar un algoritmo I-P / I-PD para suavizar la respuesta del sistema. Así mismo, si nos empeñamos en utilizar un algoritmo PI nos vemos obligados a recurrir a sintonías que utilizan el parámetro «Tf» o bien usar un algoritmo I-P.

Casi todos los métodos obtienen una respuesta adecuada y bastante fiel a la simulación y me reitero, la simulación debe ser similar a la respuesta real, de lo contrario algo falla.

Descargas

• Arduino COM Plotter
• Archivos de Arduino COM Plotter
• Librería I2CDev by Jeff Rowberg [Github]
• Librería MPU650 by Jeff Rowberg [Github]
• Simple Kalman Filter by Denys Sene [Github]
• Librería PID by Brett Beauregard [Github]

Referencias

Enlaces

• Filtro de Kalman [Wikipedia]
• Filtro complementario (inglés)
• Configurar el MPU6050 [diarioelectronicohoy]
• Introducción al algoritmo PID y su implementación en Arduino
• Tutorial MPU6050, Acelerómetro y Giroscopio [naylampmechatronics]
• Determinar la orientación con Arduino y el IMU MPU-6050 [Luis Llamas]
• Medir la inclinación con IMU, Arduino y filtro complementario [Luis Llamas]

Libros y publicaciones

[1] Aidan O’Dwyer. Handbook of PI and PID controller tuning rules, 3rd edition, Imperial College Press. ISBN: 978-1-84816-242-6

[2] Karl J. Astrom, Tore Hagglund. Control PID avanzado, Pearson, ISBN: 978-84-8322-511-0

[3] Daniel Chuck. Los sistemas de primer orden y los controladores PID, edición 2012. [Link] [Link2]

[4] J.G. Ziegler, N.B. Nichols. Optimum Settings For Automatic Controllers, 1942 edition, American Society of Mechanical Engineers. [Link]

[5] G.H. Cohen, G.A. Coon. Theoretical Consideration of Retarded Control, 1953 edition, American Society of Mechanical Engineers. [Link] [Link2]

[6] Daniel E. Rivera. Internal Model Control: A Comprehensive View, 1999 edition, College of Engineering and Applied Sciences. [Link]

[7] R. Vilanova, A. Visioli. PID Control in the Third Millennium. Chapter 5, The SIMC Method for smooth PID Controller Tuning, Springer. ISBN: 978-1-4471-2424-5.

[8] Chriss Grimholt, Sigurd Skogestad. The improved SIMC method for PI controller tuning, IFAC-conference PID’12, Brescia, Italy, March 2012. [Link]

[9] Guillermo J. Silva, Aniruddha Datta, S.P. Bhattacharyya. PID Controllers for Time-Delay Systems. Chapter 10, Analysis of Some PID Tunning Techniques. Birkhäuser. ISBN: 0-8176-4266-8