Modelado y Control de Posición de un Servo Simulado (2ªParte)

Introducción

Esta es la segunda parte del control del servo simulado. En la primera parte modelamos y sintonizamos un control de velocidad. El control de velocidad a excepción de la ausencia de tiempo muerto, no tuvo mayor complicación, nos enfrentamos a un proceso con respuesta autorregulada fácil de identificar y sintonizar. Ahora es el turno de controlar la posición y afrontar una respuesta completamente diferente, ¿no te lo crees? Pues sigue leyendo.

Funcionamiento

Recordemos que disponemos de un servo de 5 voltios que en su eje lleva acoplado un disco graduado entre 0 y 360 grados. El voltaje aplicado sobre el motor hace que éste gire en un sentido de forma continua pudiéndose invertir la polaridad para que el servo gire en sentido contrario. A medida que aplicamos más voltaje, más rápido gira el disco.

Control de Posición

Atendiendo al simulador, el rango de la posición (PV) va de 0 a 359 grados y el voltaje del motor (OP) va de -5 a 5 voltios. El voltaje positivo y negativo hace que el servo pueda girar en ambos sentidos pero como punto de consigna (SP) sólo admite grados positivos.

Identificación

Tras jugar un poco con el simulador enseguida llegamos a la conclusión de que nos enfrentamos a un integrador puro en el que cada nivel de tensión produce una nueva velocidad constante, y por tanto, la posición crece linealmente en el tiempo.

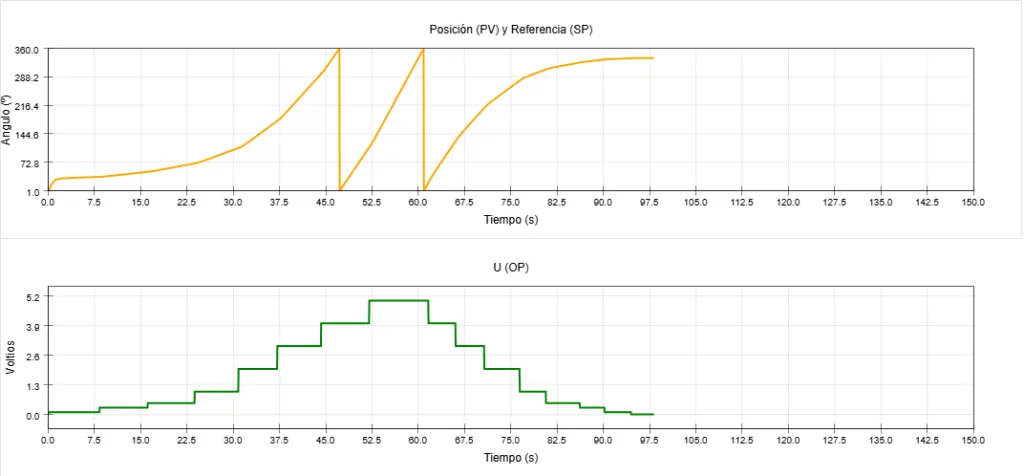
Mediante un script de Python se ha identificado que la posición crece a una velocidad proporcional al voltaje aplicado, y esa proporción es de aproximadamente 5.72 º/s por voltio.

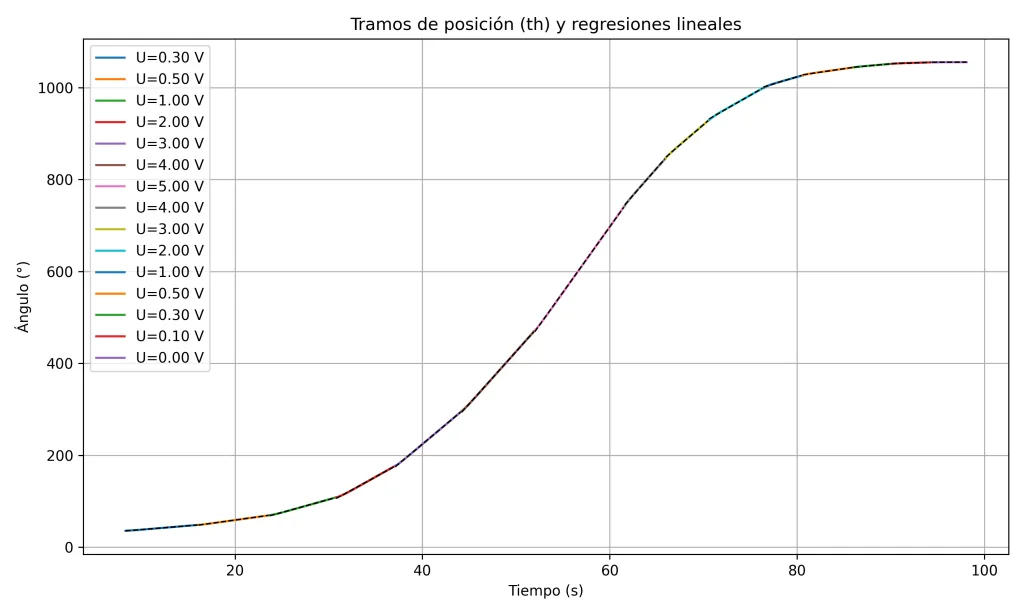
Una vez obtenida la pendiente estamos en disposición de hallar varias sintonías que en esta ocasión he añadido en dos partes, Lambda y Servo.

Lambda	Tf=1s	Tf=2s	Tf=3s	Tf=5s
Kc	0.17	0.35	0.52	0.87
Ti	1	2	3	5
Td	0	0	0	0

Servo	PI	PID
Kc	0.14	0.21
Ti	1.5	2
Td	0	0.5

Resultados

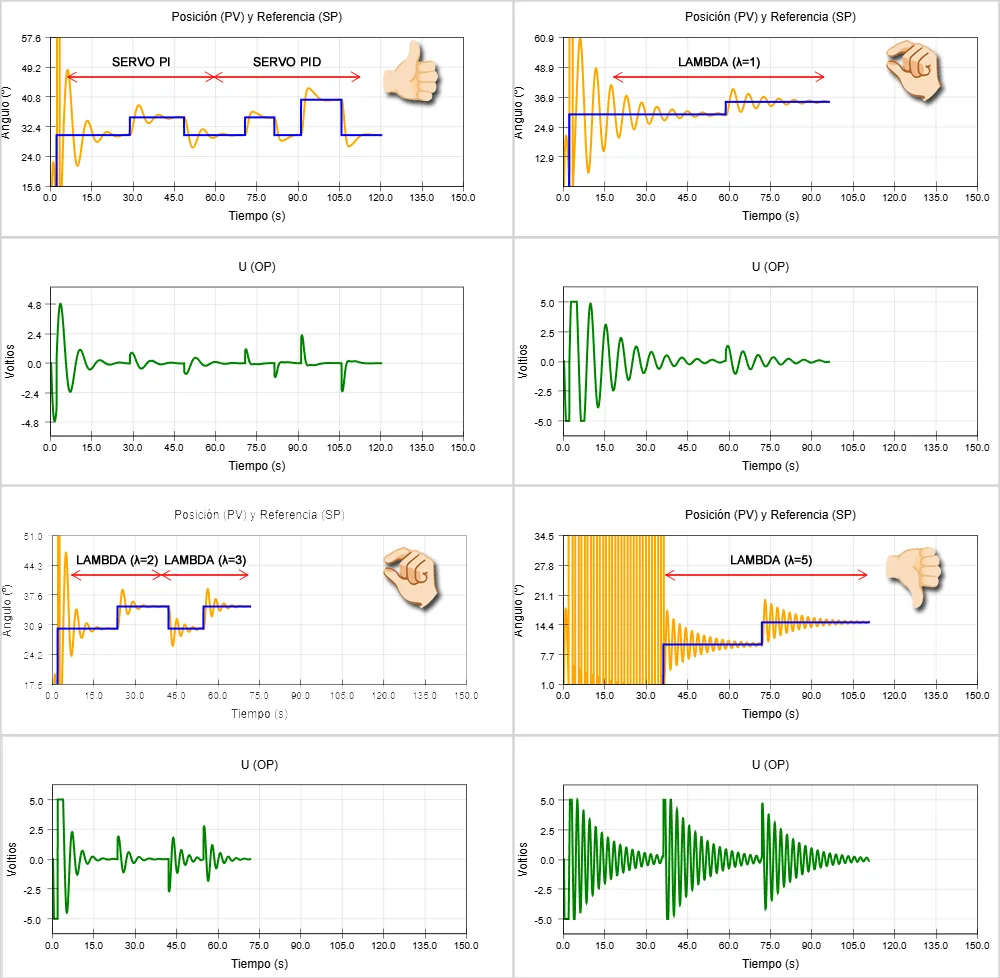
Lambda:

• Tf = 1: respuesta rápida, pero demasiado agresiva lo que provoca oscilaciones considerables tanto en la posición (PV) como en la salida (OP).

• Tf = 2 y 3: similar a la sintonía con Tf=1 aunque con pequeñas oscilaciones y tiempos de asentamiento más largos.

• Tf = 5: respuesta muy lenta, tarda demasiado en alcanzar el punto de consigna haciendo que la señal oscile en exceso.

Servo:

• PI: consigue un buen equilibrio entre velocidad y estabilidad, sin sobresaltos ni oscilaciones excesivas.

• PID: mejora el seguimiento del punto de consigna de forma más precisa, con algo más de movimiento de la salida (OP), pero sin inestabilidad.

Código Python

Identificacion_v2.py

Al ejecutar el script aparecerá un cuadro de diálogo preguntando por el archivo .m. Tras la ejecución nos devuelve dos imágenes png y un txt con los resultados.

import re
import numpy as np
import matplotlib.pyplot as plt
import os
from tkinter import Tk, filedialog
from sklearn.linear_model import LinearRegression

def corregir_salto_angular(th):
    th_corr = th.copy()
    for i in range(1, len(th_corr)):
        if th_corr[i] - th_corr[i - 1] < -300:
            th_corr[i:] += 360
    return th_corr

# --- Selección de archivo ---
Tk().withdraw()
ruta_archivo = filedialog.askopenfilename(
    title="Selecciona el archivo .m con datos",
    filetypes=[("Archivos MATLAB", "*.m")]
)

if not ruta_archivo:
    raise FileNotFoundError("No se seleccionó ningún archivo.")

base_name = os.path.splitext(os.path.basename(ruta_archivo))[0]
nombre_txt = f"{base_name}_modelo.txt"

with open(ruta_archivo, "r", encoding="utf-8") as f:
    contenido = f.read()

coincidencias = re.findall(r"data\s*=\s*\[([\s\S]+?)\];", contenido)
if not coincidencias:
    raise ValueError("No se encontró el bloque 'data = [...]' en el archivo.")

filas = coincidencias[0].strip().split("\n")
datos = np.array([[float(val) for val in fila.strip().split()] for fila in filas])

# Asignar columnas
t, th, w, u, ref = datos.T
th = corregir_salto_angular(th)

# --- Análisis de tramos ---
eps = 1e-3
cambios = np.where(np.abs(np.diff(u)) > eps)[0] + 1
segmentos = [(0, cambios[0])] + [(cambios[i], cambios[i + 1]) for i in range(len(cambios) - 1)] + [(cambios[-1], len(u))]
segmentos = segmentos[1:]  # Eliminar arranque

ganancias = []

plt.figure(figsize=(10, 6))
for i, (ini, fin) in enumerate(segmentos, start=1):
    t_seg = t[ini:fin]
    th_seg = th[ini:fin]
    u_val = u[ini]

    if len(t_seg) < 5:
        continue

    model = LinearRegression()
    model.fit(t_seg.reshape(-1, 1), th_seg)
    pendiente = model.coef_[0]
    th_fit = model.predict(t_seg.reshape(-1, 1))

    ganancias.append((i, u_val, pendiente))

    # Graficar
    plt.plot(t_seg, th_seg, label=f'U={u_val:.2f} V')
    plt.plot(t_seg, th_fit, linestyle='--', linewidth=1, color='black')

plt.title("Tramos de posición (th) y regresiones lineales")
plt.xlabel("Tiempo (s)")
plt.ylabel("Ángulo (°)")
plt.legend()
plt.grid()
plt.tight_layout()
plt.savefig(f"{base_name}_tramos.png", dpi=300)
plt.show()

# --- Modelo global ---
if ganancias:
    U_vals, vel = zip(*[(u, p) for _, u, p in ganancias])
    modelo = LinearRegression().fit(np.array(U_vals).reshape(-1, 1), np.array(vel))
    K = modelo.coef_[0]

    with open(nombre_txt, "w", encoding="utf-8") as ftxt:
        ftxt.write("MODELO IDENTIFICADO\n")
        ftxt.write("-------------------\n")
        ftxt.write(f"G(s) = {K:.4f} / s\n\n")

        ftxt.write("GANANCIAS POR TRAMO\n")
        ftxt.write("-------------------\n")
        for tramo, u_val, pend in ganancias:
            ftxt.write(f"Tramo {tramo}: U = {u_val:.2f} V → Velocidad ≈ {pend:.2f} °/s\n")
        
        ftxt.write("\nSINTONÍAS RECOMENDADAS\n")
        ftxt.write("-----------------------\n")

        # Sintonía LAMBDA (PI)
        ftxt.write("Método LAMBDA (PI puro)\n")
        for lam in [1, 2, 3, 5]:
            Kc = lam / K
            Ti = lam
            ftxt.write(f"λ = {lam:.1f} → Kc = {Kc:.4f}, Ti = {Ti:.4f}, Td = 0\n")

        # Sintonía tipo SERVO PI
        Kc_servo_PI = 0.8 / K
        Ti_servo_PI = 1.5
        ftxt.write("\nTipo SERVO (PI)\n")
        ftxt.write(f"Kc = {Kc_servo_PI:.4f}, Ti = {Ti_servo_PI:.4f}, Td = 0\n")

        # Sintonía tipo SERVO PID
        Kc_servo_PID = 1.2 / K
        Ti_servo_PID = 2
        Td_servo_PID = 0.5
        ftxt.write("\nTipo SERVO (PID)\n")
        ftxt.write(f"Kc = {Kc_servo_PID:.4f}, Ti = {Ti_servo_PID:.4f}, Td = {Td_servo_PID:.4f}\n")

    print(f"\nModelo estimado: G(s) = {K:.2f} / s")
    print(f"Archivo generado: {nombre_txt} + gráfico PNG")
else:
    print("No se obtuvieron tramos válidos.")

Enlaces

• Simulador [garikoitz.info]
• Carpeta del Proyecto [garikoitz.info]
• Respuesta integradora [garikoitz.info]
• Laboratorio virtuales [Unilabs] [Simulador]
• Modelado y Control de Velocidad de un servo simulado (1ªparte) [garikoitz.info]