Modelado y Control de Velocidad de un Servo Simulado (1ªParte)

2 abril, 2025 Garikoitz Martínez Moreno Comentarios 0 comentarios

Índice

Introducción

Se trata de un simulador desarrollado por la UNED para sus laboratorios virtuales los cuales, nos permiten descargar y ejecutar localmente la aplicación realizada en html+javascript para practicar. El simulador está muy logrado e implementa el funcionamiento de la maqueta con bastante detalle aunque he tenido que modificar parte del código javascript ya que no funcionaba la parte de guardar los datos. Podéis probarlo aquí.

El Simulador

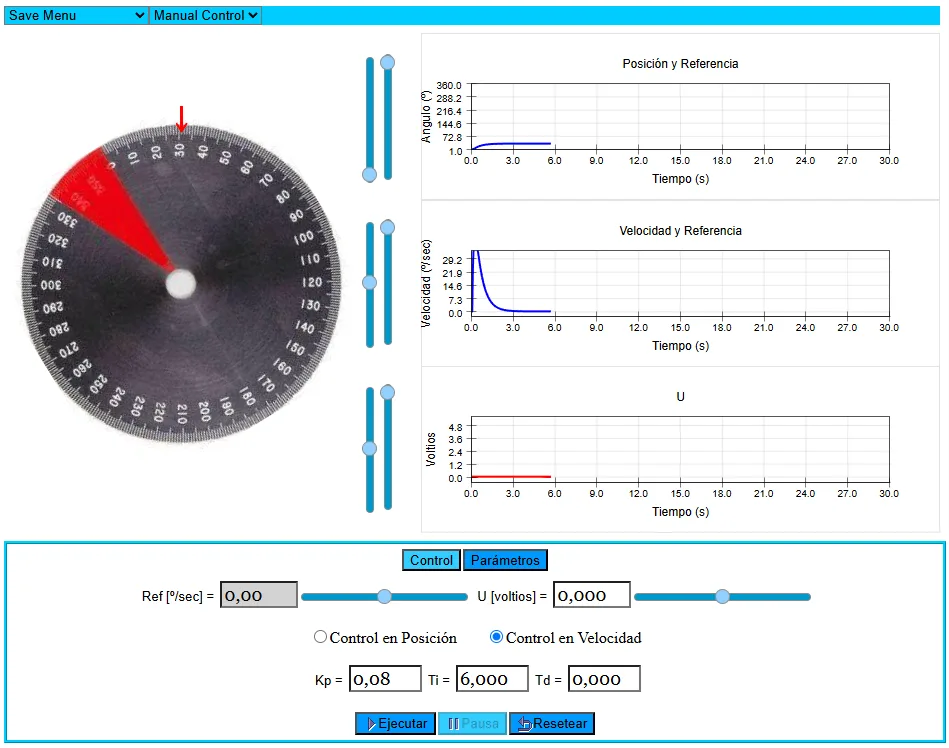
La interfaz es muy intuitiva. En la parte izquierda tenemos el disco graduado simulado. En la parte derecha tenemos las diferentes gráficas para ver la evolución de los parámetros y en la parte inferior tenemos los parámetros del PID y el control de la simulación. Cada vez que modificamos un parámetro la caja de texto se pone en amarillo y debemos pulsar la tecla «enter» para que tenga efecto. Ya que siempre uso unos términos específicos en todas mis maquetas PID os voy a poner la correspondencia de parámetros aunque entiendo que son muy intuitivos.

Ref = SP (Punto de consigna o SetPoint)
U = OP (en términos académicos la U siempre se refiere a la salida del controlador)
Kp = Kc (creo más acertado llamar Kc a la ganancia del controlador)
Posición = PV (en el control de posición)
Velocidad = PV (en el control de velocidad)

Funcionamiento

Disponemos de un servo de 5 voltios que en su eje lleva acoplado un disco graduado entre 0 y 360 grados. El voltaje aplicado sobre el motor hace que éste gire en un sentido de forma continua pudiéndose invertir la polaridad para que el motor gire en sentido contrario. A medida que aplicamos más voltaje, más rápido gira el disco.

Control de Velocidad

Atendiendo al simulador, el rango de la velocidad (PV) va de -30 a 30 º/s y el voltaje del motor (OP) va de -5 a 5 V.

Identificación

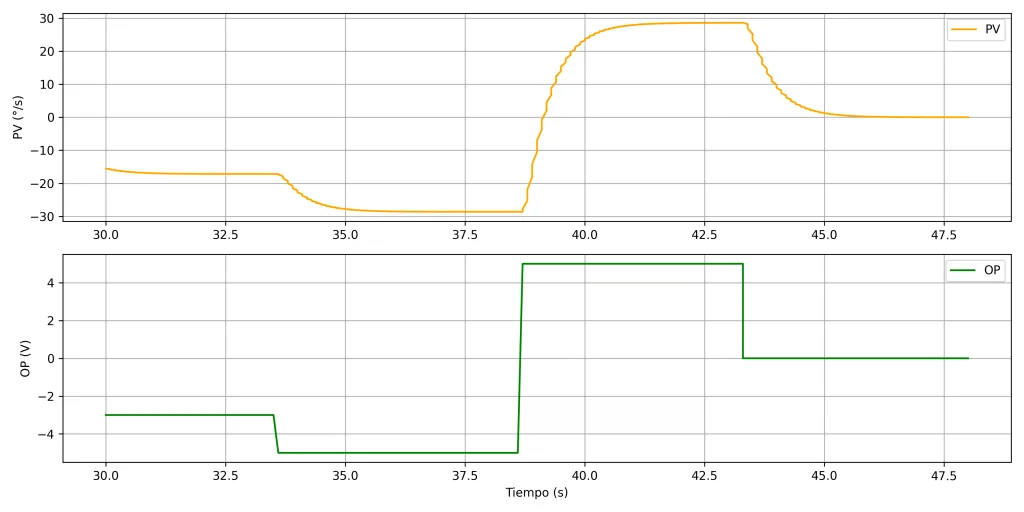
Con el control en manual y en reposo introducimos un voltaje y observamos la respuesta de la velocidad. Por suerte para nosotros la velocidad muestra una respuesta de primer orden, o dicho de otro modo, estamos antes una respuesta autorregulada.

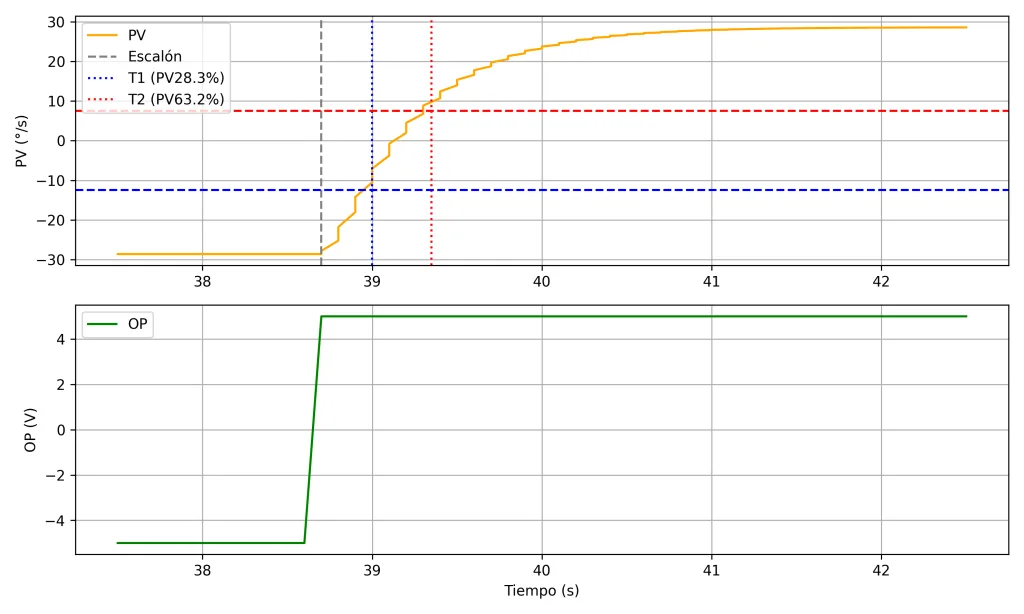
Imagen 2 – StepTest. Imagen creada con el script Graficar_velocidad.py

Aprovechando que estamos ante una respuesta autorregulada vamos a realizar la identificación del sistema mediante el método de T1 y T2 para hallar T₀ y T_p. Tanto para generar la gráfica PV/OP como para la identificación he creado dos sencillos scripts de Python que os dejo en la carpeta del proyecto.

Una característica interesante de esta identificación es la ausencia de tiempo muerto. Si os fijáis en la imagen 3, podéis apreciar que en el momento en que se realiza el salto en la OP comienza a reaccionar la PV. En cualquier proceso existe cierto retardo aunque en esta simulación no se ha tenido en cuenta. En casos así, lo correcto es tomar el tiempo de muestreo como tiempo muerto y es de ahí de donde salen los 50 ms de T₀. Las sintonías calculadas con estas constantes dan resultados con ganancias muy grandes lo que hace que tengamos que descartar los «métodos clásicos» como Ziegler Nichols o Cohen Coon.

Kp	0,95	%/%
T₀	0,05	segundos
T_p	0,52	segundos

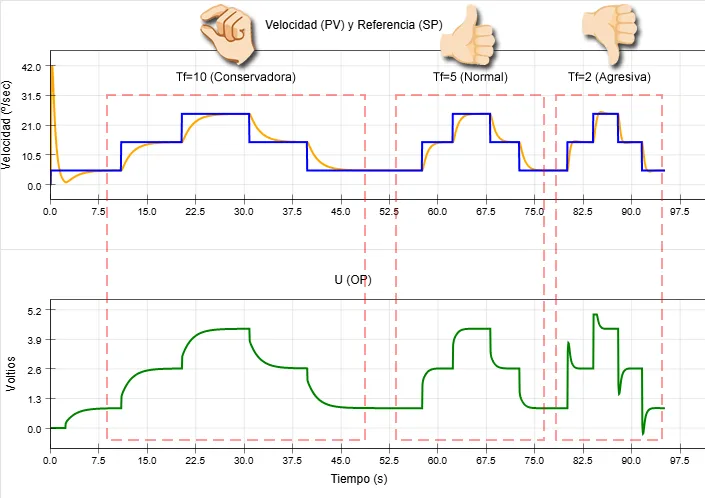
Por tanto, el mejor ajuste lo podemos obtener con las sintonías Lambda e IMC, ya que mediante la constante de tiempo deseado en lazo cerrado (λ o Tf) podemos retocar la respuesta según nuestras necesidades.

Lambda	Tf=10s Conservadora	Tf=5s Normal	Tf=2s Agresiva
Kc	0.05	0.10	0.25
Ti	0.52s	0.52s	0.52s
Td	0.05s	0.05s	0.05s

La prueba de sintonías confirma lo esperado. La sintonía conservadora es algo lenta, la normal tiene una respuesta suave y precisa, y la agresiva presenta sobrepasamiento. La prueba de sintonías ha consistido en 4 cambiós del punto de consigna de 10º/s.

Código Python

Graficar_velocidad.py

Simplemente especificar el nombre del archivo y el script os devolverá una imagen png como la imagen 2.

import re
import numpy as np
import matplotlib.pyplot as plt
import os

# Ruta al archivo .m
ruta_archivo = "Ident_v1.m"

# Leer el contenido del archivo
with open(ruta_archivo, "r", encoding="utf-8") as f:
    contenido = f.read()

# Buscar el bloque que contiene los datos
coincidencias = re.findall(r"data\s*=\s*\[([\s\S]+?)\];", contenido)

if not coincidencias:
    raise ValueError("No se encontró el bloque de datos en el archivo.")

# Procesar las filas de datos
filas = coincidencias[0].strip().split("\n")
datos = np.array([[float(valor) for valor in fila.strip().split()] for fila in filas])

# Separar columnas
t, th, w, u, ref = datos.T

# Nombre del archivo de salida PNG (mismo nombre que el .m)
nombre_base = os.path.splitext(os.path.basename(ruta_archivo))[0]
nombre_png = f"{nombre_base}.png"

# Crear la gráfica (solo velocidad y control)
plt.figure(figsize=(12, 6))

plt.subplot(2, 1, 1)
plt.plot(t, w, color='orange', label='PV')
plt.ylabel('PV (°/s)')
plt.legend()
plt.grid(True)

plt.subplot(2, 1, 2)
plt.plot(t, u, color='green', label='OP')
plt.xlabel('Tiempo (s)')
plt.ylabel('OP (V)')
plt.legend()
plt.grid(True)

plt.tight_layout()
plt.savefig(nombre_png, dpi=300)
plt.close()

print(f"Gráfica guardada como {nombre_png}")

Identificación_velocidad.py

Especificar en el script el tiempo inicial y final del salto a analizar y los rangos. Al ejecutar el script os aparecerá un cuadro de diálogo para elegir el archivo *.m de los datos y os devolverá una imagen png como la imagen 4 y un txt con la identificación.

import re
import numpy as np
import matplotlib.pyplot as plt
import os
from tkinter import Tk, filedialog

# --- OpenFileDialog para seleccionar el archivo .m ---
Tk().withdraw()
ruta_archivo = filedialog.askopenfilename(
    title="Selecciona el archivo .m",
    filetypes=[("Archivos MATLAB", "*.m")]
)

if not ruta_archivo:
    raise FileNotFoundError("No se seleccionó ningún archivo.")

# --- CONFIGURACIÓN ---
t_inicial = 37.5
t_final = 42.5

# Rango de operación
PV_min = -30
PV_max = 30
OP_min = -5
OP_max = 5

# Leer archivo
with open(ruta_archivo, "r", encoding="utf-8") as f:
    contenido = f.read()

coincidencias = re.findall(r"data\s*=\s*\[([\s\S]+?)\];", contenido)
if not coincidencias:
    raise ValueError("No se encontró el bloque de datos en el archivo.")

filas = coincidencias[0].strip().split("\n")
datos = np.array([[float(valor) for valor in fila.strip().split()] for fila in filas])
t, th, w, u, ref = datos.T

Ts = np.mean(np.diff(t))

mask = (t >= t_inicial) & (t <= t_final)
t_sel = t[mask]
w_sel = w[mask]
u_sel = u[mask]

delta_u = np.diff(u_sel)
idx_salto = np.where(np.abs(delta_u) > 0.1)[0]
if len(idx_salto) == 0:
    raise ValueError("No se detectó un escalón en el rango seleccionado.")

i_salto = idx_salto[0] + 1
t0 = t_sel[i_salto]
u_ini, u_fin = u_sel[i_salto - 1], u_sel[i_salto]
w_ini = w_sel[i_salto]
w_resp = w_sel[i_salto:]
t_resp = t_sel[i_salto:]

delta_u_val = u_fin - u_ini
delta_w_val = w_resp[-1] - w_ini
Kp = delta_w_val / delta_u_val
Kp_norm = (delta_w_val / (PV_max - PV_min)) / (delta_u_val / (OP_max - OP_min))

PV28 = w_ini + 0.283 * delta_w_val
PV63 = w_ini + 0.632 * delta_w_val

idx_t1 = np.argmax(w_resp > PV28)
idx_t2 = np.argmax(w_resp > PV63)

T1_abs = t0 + idx_t1 * Ts
T2_abs = t0 + idx_t2 * Ts

Tp = 1.5 * (T2_abs - T1_abs)
T0_abs = T2_abs - Tp
T0_rel = T0_abs - t0
T0_mostrar = Ts if T0_rel < 3 * Ts else T0_rel

# Sintonías Lambda
Ti = Tp
Tf1, Tf2, Tf3 = 4 * Tp, 10 * Tp, 20 * Tp

# PI
Kc_PI_1 = Tp / (Kp_norm * (Tf1 + T0_mostrar))
Kc_PI_2 = Tp / (Kp_norm * (Tf2 + T0_mostrar))
Kc_PI_3 = Tp / (Kp_norm * (Tf3 + T0_mostrar))

# PID
Kc_PID_1 = (Tp / (Kp_norm * (Tf1 + T0_mostrar))) * ((Tf1 + T0_mostrar) / (Tf1 + 0.5 * T0_mostrar))
Td1 = (T0_mostrar * Tf1) / (Tf1 + 0.5 * T0_mostrar)

Kc_PID_2 = (Tp / (Kp_norm * (Tf2 + T0_mostrar))) * ((Tf2 + T0_mostrar) / (Tf2 + 0.5 * T0_mostrar))
Td2 = (T0_mostrar * Tf2) / (Tf2 + 0.5 * T0_mostrar)

Kc_PID_3 = (Tp / (Kp_norm * (Tf3 + T0_mostrar))) * ((Tf3 + T0_mostrar) / (Tf3 + 0.5 * T0_mostrar))
Td3 = (T0_mostrar * Tf3) / (Tf3 + 0.5 * T0_mostrar)

# GRAFICAR
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(t_sel, w_sel, label='PV', color='orange')
plt.axvline(t0, color='gray', linestyle='--', label='Escalón')
plt.axvline(T1_abs, color='blue', linestyle=':', label='T1 (PV28.3%)')
plt.axvline(T2_abs, color='red', linestyle=':', label='T2 (PV63.2%)')
plt.axhline(PV28, color='blue', linestyle='--')
plt.axhline(PV63, color='red', linestyle='--')
plt.ylabel('PV (°/s)')
plt.legend()
plt.grid(True)

plt.subplot(2, 1, 2)
plt.plot(t_sel, u_sel, label='OP', color='green')
plt.xlabel('Tiempo (s)')
plt.ylabel('OP (V)')
plt.grid(True)
plt.legend()
plt.tight_layout()

# Guardar archivos
base_name = os.path.splitext(os.path.basename(ruta_archivo))[0]
nombre_base = f"{base_name}_identificado"
plt.savefig(f"{nombre_base}.png", dpi=300)
plt.close()

# TXT
with open(f"{nombre_base}.txt", "w", encoding="utf-8") as ftxt:
    ftxt.write("------------------------------------------------------------\n")
    ftxt.write("ACLARACIÓN SOBRE UNIDADES Y NORMALIZACIÓN\n")
    ftxt.write("------------------------------------------------------------\n")
    ftxt.write("- El modelo del sistema se identifica en unidades de ingeniería reales:\n")
    ftxt.write("    * Velocidad (PV) en grados/segundo [°/s]\n")
    ftxt.write("    * Señal de control (OP) en voltios [V]\n")
    ftxt.write("    * Tiempos en segundos [s]\n")
    ftxt.write("- Para calcular las sintonías, se normaliza usando %/%\n")
    ftxt.write("------------------------------------------------------------\n\n")

    ftxt.write("--CÁLCULOS--\n")
    ftxt.write(f"ΔOP = {delta_u_val:.3f} V\n")
    ftxt.write(f"ΔPV = {delta_w_val:.3f} °/s\n")
    ftxt.write(f"PV28 = {PV28:.3f} °/s\n")
    ftxt.write(f"PV63 = {PV63:.3f} °/s\n")
    ftxt.write(f"T1 = {T1_abs:.4f} s\n")
    ftxt.write(f"T2 = {T2_abs:.4f} s\n")
    ftxt.write(f"T0 absoluto = {T0_abs:.4f} s\n\n")

    ftxt.write("--SISTEMA--\n")
    ftxt.write(f"Kp_EU  = {Kp:.4f}\n")
    ftxt.write(f"Kp_%/% = {Kp_norm:.4f}\n")
    ftxt.write(f"T0 = {T0_mostrar:.4f} s (tiempo muerto desde el escalón)\n")
    ftxt.write(f"Tp = {Tp:.4f} s\n\n")

    ftxt.write("--SINTONÍA LAMBDA--\n")
    ftxt.write(f"Kc = {Kc_PI_1:.4f}, Ti = {Tp:.4f} Td = 0 (Tp*4)\n")
    ftxt.write(f"Kc = {Kc_PI_2:.4f}, Ti = {Tp:.4f} Td = 0 (Tp*10)\n")
    ftxt.write(f"Kc = {Kc_PI_3:.4f}, Ti = {Tp:.4f} Td = 0 (Tp*20)\n\n")

    ftxt.write(f"Kc = {Kc_PID_1:.4f}, Ti = {Tp:.4f} Td = {Td1:.4f} (Tp*4)\n")
    ftxt.write(f"Kc = {Kc_PID_2:.4f}, Ti = {Tp:.4f} Td = {Td2:.4f} (Tp*10)\n")
    ftxt.write(f"Kc = {Kc_PID_3:.4f}, Ti = {Tp:.4f} Td = {Td3:.4f} (Tp*20)\n")

print(f"Archivos generados: {nombre_base}.png y {nombre_base}.txt")

Enlaces

Simulador [garikoitz.info]
Carpeta del Proyecto [garikoitz.info]
Respuesta autorregulada [garikoitz.info]
Identificación de procesos en lazo abierto [garikoitz.info]
Laboratorio virtuales [Unilabs] [Simulador]
Modelado y Control de Posición de un servo simulado (2ªparte) [garikoitz.info]

Información básica sobre protección de datos
Responsable	Garikoitz Martínez Moreno +info...
Finalidad	Gestionar y moderar tus comentarios. +info...
Legitimación	Consentimiento del interesado. +info...
Destinatarios	Automattic Inc., EEUU para filtrar el spam. +info...
Derechos	Acceder, rectificar y cancelar los datos, así como otros derechos. +info...
Información adicional	Puedes consultar la información adicional y detallada sobre protección de datos en nuestra página de política de privacidad.