PID AutoTune del Firmware Marlin

Introducción

Como apasionado del algoritmo PID enseguida me llamó la atención el control de temperatura de las impresoras 3D. Indagando en el código enseguida encuentras tanto la implementación del algoritmo PID como el método de auto sintonía utilizado. El objetivo de ésta entrada es entender el funcionamiento del autotune y ver como podemos jugar con el.

El Autotune

Los métodos de auto sintonía son algoritmos ampliamente utilizados cuando lo que se busca es obtener una sintonización rápida y funcional al margen de los conocimientos del usuario final. En el firmware de Marlin es tan sencillo como hacerlo desde el display de la impresora si tenemos las opciones activadas, o usando el comando gcode M303 Ea Cb Sc, donde a hace referencia al hotend o cama caliente, b a los ciclos y c a la temperatura del test. Si por ejemplo queremos hacer el autotune de la cama caliente mediante comandos, basta con introducir mediante Pronterface, Octoprint o similar el comando:

M303 E-1 C3 S60

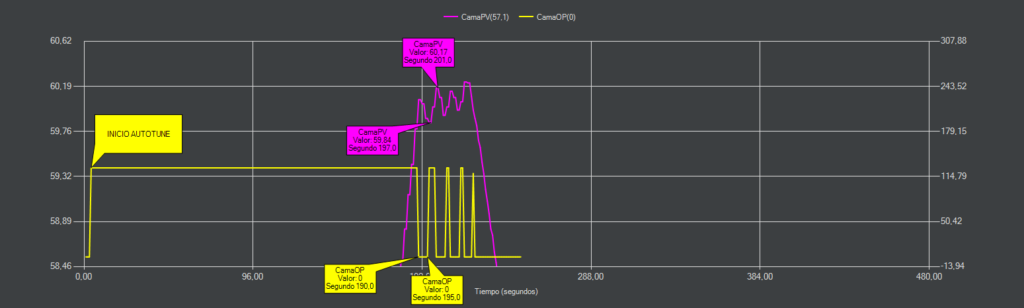
Esto nos daría un resultado del tipo:

 bias: 127 d: 127 min: 59.77 max: 60.14
 bias: 127 d: 127 min: 59.74 max: 60.10
 bias: 127 d: 127 min: 59.74 max: 60.16 Ku: 770.50 Tu: 10.10
 No overshoot
 Kp: 154.10 Ki: 30.51 Kd: 518.80
PID Autotune finished! Put the last Kp, Ki and Kd constants from below into Configuration.h
#define DEFAULT_bedKp 154.10
#define DEFAULT_bedKi 30.51
#define DEFAULT_bedKd 518.80

Con éste resultado podemos modificar el archivo Configuration.h y recompilar como se nos propone o introducir los nuevos parámetros de sintonía mediante el comando M304. Pero no solo estamos obteniendo la sintonía, además nos da toda esta información:

• La ganancia última Ku.
• El periodo de oscilación Tu.
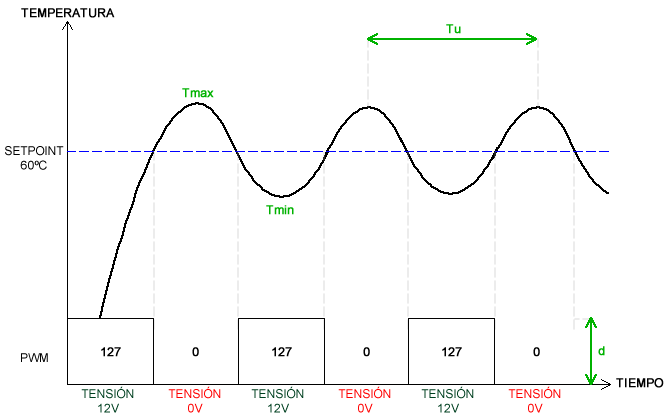
• La delta de la salida d. El 127 que vemos es la salida PWM (0-255) enviada al cartucho calefactor de la cama caliente durante la prueba, es decir, 127 = ~255/2 = ~50% = ~12V. Al menos en mi caso veo que la salida está limitada (BANG_MAX) siempre a 127.
• Las temperaturas mínima y máxima alcanzadas durante el test.
• Al indicar No overshoot podemos prever que se ha seleccionado una sintonía conservadora para evitar el sobrepasamiento.
• Las constantes de sintonía Kp, Ki y Kd.

Lo veremos más adelante pero en resumen, Ku y Tu nos van a permitir calcular más sintonías según nuestras necesidades.

Funcionamiento

El código se encuentra en el archivo «Marlin\src\module\Temperature.cpp» a partir de la línea 649 y no se trata ni más ni menos que de una identificación mediante el método del relé.

A simple vista se puede apreciar como los ciclos son de 5 segundos y el detalle del cálculo de Ku, Tu y de Kp, Ki y Kd. También nos volvemos a encontrar con la expresión «No overshoot» cuando hace referencia a la cama caliente y a una string «STR_CLASSIC_PID» cuando no se refiere a la cama caliente.

...     
      if (updateTemperaturesIfReady()) { // temp sample ready

        // Get the current temperature and constrain it
        current_temp = GHV(degChamber(), degBed(), degHotend(heater_id));
        NOLESS(maxT, current_temp);
        NOMORE(minT, current_temp);

        #if ENABLED(PRINTER_EVENT_LEDS)
          ONHEATING(start_temp, current_temp, target);
        #endif

        TERN_(HAS_FAN_LOGIC, manage_extruder_fans(ms));

        if (heating && current_temp > target && ELAPSED(ms, t2 + 5000UL)) {
          heating = false;
          SHV((bias - d) >> 1);
          t1 = ms;
          t_high = t1 - t2;
          maxT = target;
        }

        if (!heating && current_temp < target && ELAPSED(ms, t1 + 5000UL)) {
          heating = true;
          t2 = ms;
          t_low = t2 - t1;
          if (cycles > 0) {
            const long max_pow = GHV(MAX_CHAMBER_POWER, MAX_BED_POWER, PID_MAX);
            bias += (d * (t_high - t_low)) / (t_low + t_high);
            LIMIT(bias, 20, max_pow - 20);
            d = (bias > max_pow >> 1) ? max_pow - 1 - bias : bias;

            SERIAL_ECHOPGM(STR_BIAS, bias, STR_D_COLON, d, STR_T_MIN, minT, STR_T_MAX, maxT);
            if (cycles > 2) {
              const float Ku = (4.0f * d) / (float(M_PI) * (maxT - minT) * 0.5f),
                          Tu = float(t_low + t_high) * 0.001f,
                          pf = (ischamber || isbed) ? 0.2f : 0.6f,
                          df = (ischamber || isbed) ? 1.0f / 3.0f : 1.0f / 8.0f;

              tune_pid.Kp = Ku * pf;
              tune_pid.Ki = tune_pid.Kp * 2.0f / Tu;
              tune_pid.Kd = tune_pid.Kp * Tu * df;

              SERIAL_ECHOLNPGM(STR_KU, Ku, STR_TU, Tu);
              if (ischamber || isbed)
                SERIAL_ECHOLNPGM(" No overshoot");
              else
                SERIAL_ECHOLNPGM(STR_CLASSIC_PID);
              SERIAL_ECHOLNPGM(STR_KP, tune_pid.Kp, STR_KI, tune_pid.Ki, STR_KD, tune_pid.Kd);
            }
          }
          SHV((bias + d) >> 1);
          TERN_(HAS_STATUS_MESSAGE, ui.status_printf(0, F(S_FMT " %i/%i"), GET_TEXT(MSG_PID_CYCLE), cycles, ncycles));
          cycles++;
          minT = target;
        }
      }
...

Si nos fijamos en el cálculo de Ku, el denominador lo multiplica por 0.5 (lo divide por 2) porque en realidad está usando la mitad de d (127 = 255/2).

\begin{equation}
\begin{split}
& Ku = \frac{4\times d}{\pi\times a}=\frac{4\times d\times 0.5}{\pi\times (maxT-minT)\times 0.5}=\\
& \\
& =\frac{4\times 255\times 0.5}{\pi\times (60.16-59.74)\times 0.5}\approx770.5
\end{split}
\end{equation}

Tabla de sintonías

Como os adelantaba anteriormente, el disponer de Ku y Tu nos permite poder calcular más sintonías. Si os fijáis en las sintonías de Ziegler-Nichols podéis ver el cálculo de las sintonías «no overshoot» y «classic PID» que usa el firmware de Marlin. Os dejo también otras sintonías menos conocidas pero no por ello menos útiles.

En mi caso con los valores de Ku = 770,5 y Tu = 10,1 obtenidos quedaría de la siguiente manera.

Futuras mejoras

Una forma de conseguir mejores sintonías sin tener que recurrir al método de prueba y error sería realizando una identificación en lazo abierto. Para ello necesitamos poder mover nosotros la salida PWM de los cartuchos para posteriormente analizar la respuesta escalón del sistema y hallar sus constantes. Una vez modelado el sistema podemos calcular nuevas sintonías y simularlas hasta encontrar la respuesta deseada. Si tenéis curiosidad sobre como se realiza esta identificación y los beneficios que aporta, os recomiendo la lectura de la entrada «Sintonizar PID con Arduino – Balancín Simple» en especial los apartados 3.2 y 3.4 que abordan la identificación en lazo abierto y la simulación en lazo cerrado.

El firmware de Marlin parece preparado para ésta posibilidad como se puede apreciar en el archivo «Configuration.h» en la línea 697

//#define PID_OPENLOOP          // Puts PID in open loop. M104/M140 sets the output power from 0 to PID_MAX

Lamentablemente es una opción que no he visto nunca activada en ningún firmware de los que he probado y por lo que he visto en el código, puede que sea debido a que si compilas con la variable «PID_OPENLOOP» descomentada anulas el funcionamiento del PID. Sería interesante que se pudiera activar/desactivar ésta opción desde la pantalla de la impresora para poder realizar la identificación en lazo abierto (lazo en manual) y una vez terminada la identificación poder activar el funcionamiento normal del PID (lazo en automático).

Conclusiones

La implementación del autotune en el firmware de Marlin es sencillo pero efectivo y salvo que tengamos problemas en los cartuchos o en los termistores podemos resintonizar de forma rápida y segura. No lo he mencionado pero es totalmente recomendable lanzar el autotune al menos cuando montamos nuestra impresora por primera vez y cada vez que actualizamos el firmware.

Si nos fijamos un momento en las sintonías calculadas se puede ver claramente que se usa la sintonía más conservadora (no overshoot) para la cama caliente y una algo más agresiva (classic PID) para el hotend. En este aspecto la estrategia tiene sentido ya que la cama caliente sufre menos perturbaciones de temperatura, sin embargo el hotend está expuesto a un flujo de aire en ocasiones oscilante sumado al paso continuo del filamento, y una sintonía más agresiva nos ayuda a mantenernos en el punto de consigna de temperatura que necesite nuestro filamento. Ahora bien, si con la sintonía que nos propone autotune vemos que la temperatura oscila más de lo deseado siempre podemos tener a mano la tabla para buscar una opción más adecuada.

Referencias

• Firmware Marlin
• PID Tuning [RepRap]
• Sintonía de reguladores PID [Cesar Prada] [Método del relé en Pág. 140]