Sintonizar PID con Arduino – Sistema Bola-Viga
Introducción
Esta maqueta es un sistema muy empleado en el mundo educativo debido a que posee unas características que la hacen muy interesante de analizar y sintonizar. Una característica interesante es que su respuesta tiene carácter integrador, lo que conlleva recurrir a métodos de identificación en lazo cerrado y solamente eso, ya nos saca de nuestra zona de confort. En este caso implementaremos un control PID pero podemos encontrar por la red controladores más sofisticados como el LQR o el LQG.
Sistema empleado
La maqueta está realizada con piezas impresas en 3D para la ocasión y un par de varillas metálicas por donde se desliza la bola.
El funcionamiento es muy sencillo, disponemos de un micro interruptor para cambiar entre modo manual y automático, y de un potenciómetro que en modo manual mueve el ángulo del servo y por ende la inclinación de la viga (OP), y en modo automático cambia el punto de consigna (SP) de posición de la bola en la viga. El objetivo es situar una bola en una posición determinada de la viga mediante un controlador PID.
Componentes
- Sensor de distancia.
- Servomotor.
- Micro interruptor.
- Potenciómetro.
- Arduino UNO o similar.
Sensor de distancia
Investigando un poco que tipo de sensores de distancia asequibles existen para Arduino, encontré unos cuantos y muchos ejemplos de uso, pero es diferente cuando se hace una prueba de un sensor a cuando le das un uso en el que se requiere cierta precisión. De todo lo que encontré me quedo con cuatro sensores de los que os dejo una tabla comparativa.
- GP2Y0A21YK0F: Buena precisión incluso fuera de rango. Requiere calibración. Requiere objetos (en este caso bolas) de mayor dimensión para medir correctamente.
- TOF10120: Buena precisión incluso fuera de rango. La señal necesita ser tratada para hacer control con ella.
- VL53L0X: Buena precisión incluso fuera de rango. La señal necesita ser tratada para hacer control con ella.
- HC-SR04: Buena precisión incluso fuera de rango. Requiere objetos (en este caso bolas) de mayor dimensión para medir correctamente.
Con cualquiera de ellos se pueden conseguir resultados aceptables pero yo finalmente elegí el sensor VL53L0X por utilizar un sensor diferente al que solemos encontrar en este tipo de maquetas.
Servomotor

En esta ocasión he utilizado un servo MG995 con un torque de entre 8,5 y 10 Kg/cm, pero valdría cualquier otro de características similares. En la parte de programación se opera con microsegundos en lugar de con ángulos para ganar precisión.
El coste de la maqueta puede oscilar entre 30 y 50€ dependiendo del servo y Arduino elegidos.
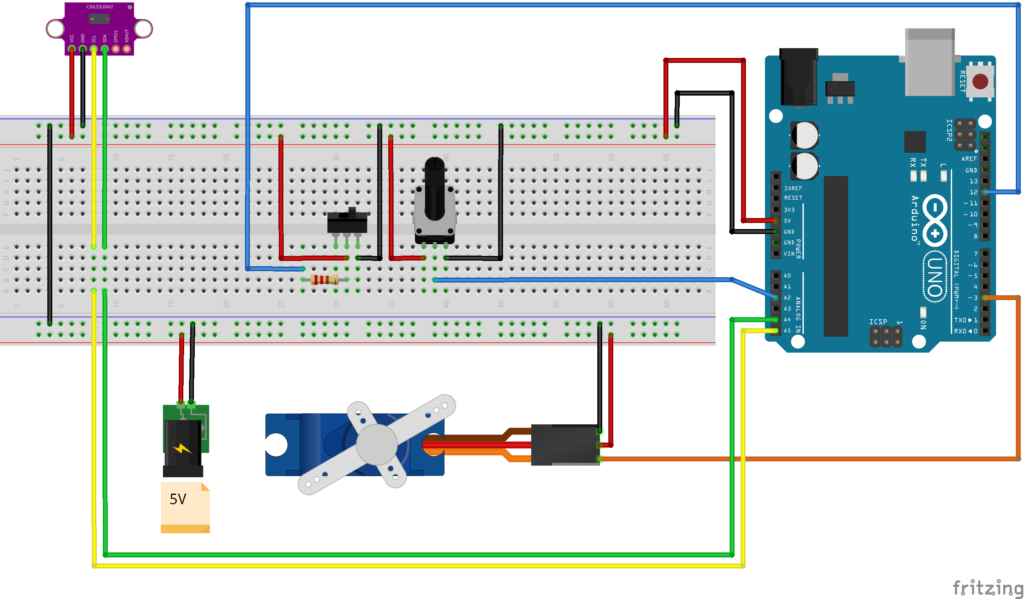
Esquema de conexiones
Código de Arduino
/***************************************************************
* Desarrollado por Garikoitz Martínez [garikoitz.info] [06/2022]
* https://garikoitz.info/blog/?p=1301
***************************************************************/
/***************************************************************
* Librerías
***************************************************************/
#include <Wire.h>
#include <PID_v1.h>
#include "Adafruit_VL53L0X.h"
#include <Servo.h>
/***************************************************************
* Variables
***************************************************************/
Servo myservo;
const int Interruptor = 12;
unsigned long previousMillis = 0;
int Ts = 50, pos = 0;
unsigned long contador = 0;
//Control PID
boolean modo = false; //false=auto true=manual
float tmp=0.0, tmp_ant=0.0, OP=0, angulo=0.0, angulo_ant=0.0, media=0.0;
double SetpointP, InputP, OutputP;
/***************************************************************
* Sintonías calculadas (Relé --> Ku=0.99 y Tu=4.6 segundos)
***************************************************************/
//double Kc=0.59, Ki=0.26, Kd=0.34; //Z-N classic PID
//double Kc=0.69, Ki=0.38, Kd=0.48; //Z-N Pessen Integral Rule
//double Kc=0.33, Ki=0.14, Kd=0.49; //Z-N some overshoot
//double Kc=0.20, Ki=0.09, Kd=0.30; //Z-N no overshoot
//double Kc=0.33, Ki=0.07, Kd=0.15; //Farrington
//double Kc=0.49, Ki=0.11, Kd=0.57; //Farrington
//double Kc=0.53, Ki=0.12, Kd=0.49; //McAvoy and Johnson
//double Kc=0.25, Ki=0.07, Kd=0.28; //Atkinson and Davey (20% overshoot)
//double Kc=0.99, Ki=0.43, Kd=0.57; //Pettit and Carr (Underdamped)
//double Kc=0.66, Ki=0.14, Kd=0.50; //Pettit and Carr (Critically damped)
//double Kc=0.49, Ki=0.07, Kd=0.38; //Pettit and Carr (Overdamped)
//double Kc=0.44, Ki=0.16, Kd=0.38; //Tinham (Less than quarter decay ratio response)
//double Kc=0.74, Ki=0.26, Kd=0.34; //Corripio (Quarter decay ratio)
//double Kc=0.62, Ki=0.27, Kd=0.24; //ABB (P+D tuning rule)
//double Kc=0.45, Ki=0.04, Kd=0.33; //Tyreus and Luyben
//double Kc=0.33, Ki=0.14, Kd=0.19; //Yu (Some overshoot)
//double Kc=0.20, Ki=0.09, Kd=0.11; //Yu (No overshoot)
//double Kc=0.74, Ki=0.26, Kd=0.34; //Smith
//double Kc=0.99, Ki=0.34, Kd=0.45; //Alfaro Ruiz (Quarter decay ratio)
//double Kc=1.65, Ki=0.57, Kd=0.76; //Alfaro Ruiz (Quarter decay ratio)
//double Kc=0.39, Ki=0.09, Kd=0.29; //Lloyd (Non self-regulating processes)
//double Kc=0.59, Ki=0.26, Kd=0.33; //NI Labview (Quarter decay ratio)
//double Kc=0.25, Ki=0.11, Kd=0.14; //NI Labview (Some overshoot)
//double Kc=0.15, Ki=0.06, Kd=0.08; //NI Labview (Little overshoot)
//---------------------------------------------------------------
double Kc=0.45, Ki=0.1, Kd=0.35; //Tyreus and Luyben mod
//---------------------------------------------------------------
PID myPID(&InputP, &OutputP, &SetpointP, Kc, Ki, Kd,P_ON_E, REVERSE);//PI-D
//PID myPID(&InputP, &OutputP, &SetpointP, Kc, Ki, Kd,P_ON_M, REVERSE); //I-PD
//
Adafruit_VL53L0X lox = Adafruit_VL53L0X();
/***************************************************************
* SETUP
***************************************************************/
void setup()
{
Wire.begin();
if (!lox.begin()) {
Serial.println(F("Error al conectar al sensor VL53L0X"));
while(1);
}
lox.startRangeContinuous();
myservo.attach(3); // asignamos el pin al servo.
Serial.begin(9600);
myPID.SetOutputLimits(0, 100);
SetpointP = 70;
}
/***************************************************************
* BUCLE PRINCIPAL
***************************************************************/
void loop()
{
VL53L0X_RangingMeasurementData_t measure;
lox.rangingTest(&measure, false);
if (measure.RangeStatus != 4) {
//media = measure.RangeMilliMeter;
media = Rolling_avg(measure.RangeMilliMeter);
media = media * 0.1; //Pasamos a cm
}
if (millis() - previousMillis > Ts) //Bucle de control cada Ts milisegundos
{
previousMillis = millis();
contador +=1;
if (digitalRead(12) == HIGH){
modo=true; //Modo Manual
myPID.SetMode(MANUAL);
}else{
modo=false; //Modo Automático
myPID.SetMode(AUTOMATIC);
}
InputP = mapf(media, 2, 26, 0, 100); //PV en cm a porcentaje
//InputP = media;
/***************************************************************
* Modo MANUAL - Potenciómetro ---> Ángulo Servo
***************************************************************/
if (modo==true){
//----------------------
// Método del Relé
//----------------------
if (1){
if (InputP <60){
pos=950; //arriba -> bola hacia la izq
myservo.writeMicroseconds(pos);
}else if (InputP >60){
pos=1475; //abajo -> bola hacia la dcha
myservo.writeMicroseconds(pos);
}
OP = mapf(pos, 850, 1575, 0, 100);
}
//----------------------
// Potenciómetro
//----------------------
if (0){
SetpointP=0;
tmp = analogRead(A1);
tmp = mapf(tmp, 1023.0, 0.0, 850, 1575); // escalamos potenciometro al servo
if(abs(tmp-tmp_ant)>1){
angulo = tmp;
}
tmp_ant=angulo;
OP = mapf(tmp,850, 1575, 0, 100);
if (angulo>=850 || angulo<=1575) myservo.writeMicroseconds(angulo);
}
/***************************************************************
* DEBUG PUERTO SERIE (Para Arduino COM Plotter)
***************************************************************/
Serial.print("#"); //Char inicio
Serial.print(0); //SP
Serial.write(" "); //Char separador
Serial.print(InputP,0); //PV InputP
Serial.write(" "); //Char separador
Serial.print(OP,0); //OP
Serial.println();
}
/***************************************************************
* Modo AUTOMÁTICO - PID
***************************************************************/
if (modo==false){
if (0){ //SetPoint mediante Potenciómetro
tmp = analogRead(A1);
tmp = mapf(tmp, 0.0, 1023.0, 0, 100);
if(abs(tmp-tmp_ant)>4){
SetpointP = tmp;
}
tmp_ant=SetpointP;
}
if (1){
// SetpointP automatizado
if (contador < 1000) SetpointP = 70;
if (contador >= 1000 && contador < 2000) SetpointP = 60;
if (contador >= 2000 && contador < 3000) SetpointP = 50;
if (contador >= 3000 && contador < 4000) SetpointP = 60;
if (contador > 4000) contador = 0;
}
angulo = mapf(OutputP, 0, 100, 850, 1575);
if (abs(SetpointP-InputP)>5){ //Banda muerta del 5%
myPID.Compute();
myservo.writeMicroseconds(angulo);
angulo_ant = angulo;
}else{
myservo.writeMicroseconds(angulo_ant);
}
/***************************************************************
* DEBUG PUERTO SERIE (Para Arduino COM Plotter)
***************************************************************/
Serial.print("#"); //Char inicio
Serial.print(SetpointP,0); //SP
Serial.write(" "); //Char separador
Serial.print(InputP,0); //PV
Serial.write(" "); //Char separador
Serial.print(OutputP,0); //OP
Serial.println();
}
}//millis
}//Loop
/***************************************************************
* FUNCIONES
***************************************************************/
//Función MAP adaptada a punto flotante.
double mapf(double val, double in_min, double in_max, double out_min, double out_max) {
return (val - in_min) * (out_max - out_min) / (in_max - in_min) + out_min;
}
//High-pass Filter
//A low α will be very slow to rapid input changes and take many samples into account.
//A high α will be fast, but average over fewer samples. You can look at α as kind of a cutoff frequency in a low-pass filter.
//OP = HPS(tmp,0.1,EMA_s_pot);
//OP = tmp-EMA_s_pot;
double HPS(double sensorValue, float EMA_a, int EMA_S) {
return (EMA_a*sensorValue) + ((1-EMA_a)*EMA_S);
}
//Función Promedio
float Rolling_avg(float value) {
const byte nvalues = 10; // Moving average window size
static byte current = 0; // Index for current value
static byte cvalues = 0; // Count of values read (<= nvalues)
static float sum = 0; // Rolling sum
static float values[nvalues];
sum += value;
if (cvalues == nvalues)
sum -= values[current];
values[current] = value; // Replace the oldest with the latest
if (++current >= nvalues)
current = 0;
if (cvalues < nvalues)
cvalues += 1;
return sum/cvalues;
}
Adecuando la señal del sensor
La señal del sensor por defecto presenta bastante ruido por lo que para hacer control con ella he optado en esta ocasión por la implementación de una función promedio que nos devuelve una señal más limpia. En realidad la función realiza una media móvil en la que podemos especificar el número de medidas que intervienen para adecuar el resultado a nuestras necesidades.
Identificación del sistema
Como hemos comentado, la identificación es diferente a maquetas anteriores debido a que tiene un comportamiento integrador, me explico, si alteramos el ángulo de la viga la bola se moverá en una dirección y no parará. En maquetas anteriores los sistemas tenían respuesta autorregulada, lo que les hacía llegar a una situación estable con el tiempo ante cualquier alteración.
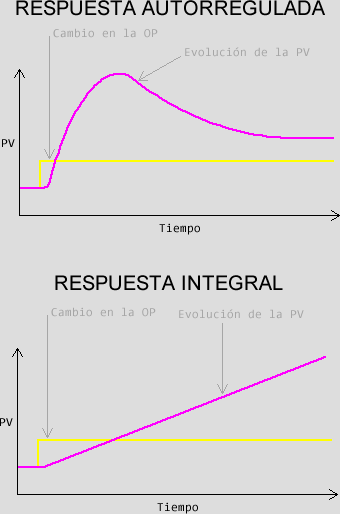
¿Qué significa esto?, pues que principalmente no podemos recurrir a realizar una identificación de saltos escalón (en lazo abierto) y obtener las constantes del sistema como en maquetas anteriores, nos vemos obligados a recurrir a otras técnicas de lazo cerrado como el de oscilación mantenida de Ziegler y Nichols o el del relé de Aström y Hägglund.
Método del relé de Aström y Hägglund
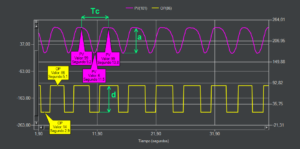
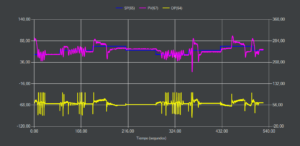
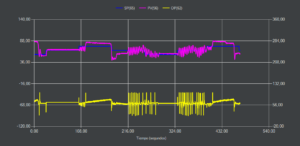
Este método consiste en programar un relé, en nuestro caso moviendo el servo de igual forma en ambos sentidos. Lo interesante es conseguir la oscilación continua sin llegar a los límites 0-100% de la PV. Del ensayo obtenemos 3 datos que nos sirven para estimar las ganancias del controlador PID, la amplitud de la PV (a), la amplitud de la OP (d) y el periodo de oscilación (Tc). Se ha usado un relé ideal sin histéresis.
Los datos obtenidos del ensayo son a = 93%, d = 72% y Tc = 4,6 segundos, con los cuales calcularemos la ganancia última Ku y el periodo de oscilación último Tu.
\begin{align}
& Ku = \frac{4d}{\pi a}=\frac{4\times 72}{\pi\times 93}=0.99\\
& Tu = Tc = 4.6 segundos
\end{align}Con Ku y Tu podemos calcular la sintonía del controlador siguiendo las reglas de Ziegler y Nichols entre otras.
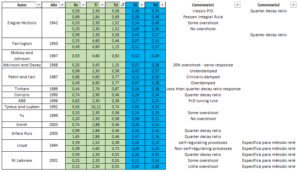
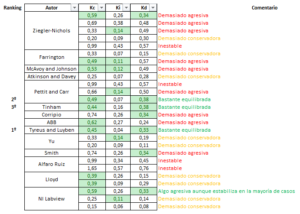
Sintonías resultantes
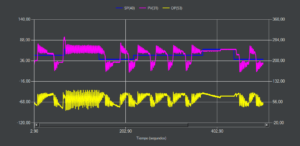
Resultados
Me gustaría aprovechar la ocasión para recordar que las sintonías calculadas ya sea en lazo abierto como en lazo cerrado son un punto de partida de las que con pequeños retoques se consigue la sintonía «final». Este es el ejemplo perfecto ya que la mayoría de las sintonías necesitan retocar alguno de los términos para que el resultado sea aceptable.
A continuación unos comentarios sobre tres sintonías.
Z-N (Pessen Integral Rule) (PI-D)
La combinación de alta ganancia integral y derivativa hace que el servo se mueva demasiado, no consiguiendo estabilizar cerca del setpoint en la mayoría de los casos.
Pettit and Carr (PI-D)
Se aprecia una gran mejoría comparada con la anterior aunque da la impresión de que la ganancia integral es algo pequeña.
Tyreus and Luyben (PI-D)
Es la sintonía que mejores resultados arroja aunque le falta un poco de ganancia integral. Aún así, dependiendo de donde queramos estabilizar la bola, no siempre conseguimos una estabilidad total.
Al probar las sintonías he llegado a la conclusión de que nos podemos mover entre:
\begin{align}
& 0.3\leq K{c} \leq 0.65\\
& 0.1\leq K{i} \leq 0.15\\
& 0.3\leq K{d} \leq 0.45\\
\end{align}Conclusiones
Tengo que reconocer que llevaba tiempo detrás de la realización de esta maqueta y que como esperaba, ha sido puro disfrute. Ya inicialmente, el que no sea un sistema auto regulado nos hace salir de la zona de confort e ingeniárnoslas para programar un relé y empezar a obtener sintonías. Una vez que tenemos las sintonías, nos vemos obligados a probar varias para familiarizarnos con el punto en que podemos considerar las ganancias altas o bajas y conseguir resultados aceptables.
La verdad es que es una maqueta en la que es difícil presentar unos resultados «bonitos» en cuanto a las gráficas se refiere. No es difícil de estabilizar la bola en el centro, de hecho, mediante prueba error podemos obtener una sintonía decente en pocos minutos, pero ya sabéis que lo que realmente me interesa es la obtención de sintonías mediante métodos analíticos.
Descargas
- Archivos del proyecto (1.69MB) [Descargar] [Carpeta]
- Fuentes impresión 3D. Los archivos 3D son modificaciones de los creados por Henar Brenlla para su proyecto fin de grado. Os dejo mis STLs y los archivos fuente de Solid Edge.
- Esquema de conexiones Fritzing.
- Código de Arduino.
- Excel con las sintonías calculadas.
Referencias
Enlaces
- Arduino Com Plotter (ACP) [garikoitz.info]
- Control PID de Barra y Bola con Arduino [Estudio Roble]
- PID Seesaw part 1 and part 2 [Norwegian Creations]
- Control distancia pelota [Henar Brenlla]
- Balancing of a Ball on Beam using Arduino as a PID controller [Mechatronics Tutorials]
- TOF10120 laser Rangefinder interfacing & code [Engr Fahad]
- Ajuste empírico de controladores PID- Método del relé (pág. 14) [Fernando Morilla]
- Identificación de procesos sobreamortiguados utilizando técnicas de lazo cerrado [Víctor M. Alfaro]
- Introducción al algoritmo PID y su implementación en Arduino [garikoitz.info]
Libros y Publicaciones
[1] Karl J. Astrom, Tore Hagglund. Control PID avanzado, Pearson, ISBN: 978-84-8322-511-0
[2] Myke King. «Process Control – A Practical Approach«, 2nd Edition, Chapter 2.4, Integrating Processes and Chapter 3.23, Suggested Tuning Method for Integrating Processes, Wiley, ISBN: 9781119157755
[3] O’Dwyer, Aidan. Handbook of PI and PID Controller Tuning Rules. 3rd Edition, Chapter 3.10, Non-Model Specific. Imperial College Press, ISBN: 978-1-84816-242-6