Regresión Lineal y No Lineal – Excel VS .Net
Introducción
La ecuación de Antoine es utilizada para obtener el valor de la presión de vapor (P) en función de la temperatura (T) para componentes puros y se basa en una correlación de tres parámetros A, B y C. Dicho esto, el objetivo de esta entrada es obtener los coeficientes de la ecuación de Antoine para un rango de temperaturas y presiones concretos dada la ecuación 1.
\begin{align}
& log(P) = A-B / (T + C)
\end{align}Para ello utilizaremos Excel como herramienta básica que casi todos conoceréis y tendréis instalada en vuestro equipo y además veremos como afrontar este tipo de problemas en .NET con la ayuda de una librería externa bastante interesante como es Accord.
No es la intención de esta entrada profundizar en conceptos matemáticos complejos ni entrar en detalle en el concepto de regresión, más bien se pretende dar unas pinceladas para poder ser capaces de plantear y resolver problemas similares.
Datos
| Temperatura (ºF) | Presión (psia) |
| 65,44 | 41,17 |
| 73,78 | 47,32 |
| 82,11 | 54,15 |
| 90,45 | 61,70 |
| 98,78 | 70,02 |
| 107,12 | 79,15 |
| 115,46 | 89,14 |
| 123,79 | 100,03 |
| 132,13 | 111,87 |
| 140,46 | 124,70 |
| 148,80 | 138,58 |
| 157,13 | 153,54 |
| 165,47 | 169,64 |
| 173,80 | 186,90 |
| 182,14 | 205,39 |
Regresión Lineal
La ecuación de Antoine no es lineal, por lo que para plantear la solución lineal lo primero es «linealizar» dicha ecuación.
\begin{align}
& log(P) = A-B / (T + C)\\ & T * log(P) + C * log(P) = A * T + A * C - B\\ & log(P) = A + (A * C - B) / T - C * log(P) / T
\end{align}Planteamos la ecuación 4 como polinómica.
\begin{align}
& y = a0 + a1 * x1 + a2 * x2\\
& y = log(P)\\
& x1 = 1 / T \\
& x2 = log(P) / T
\end{align}Excel
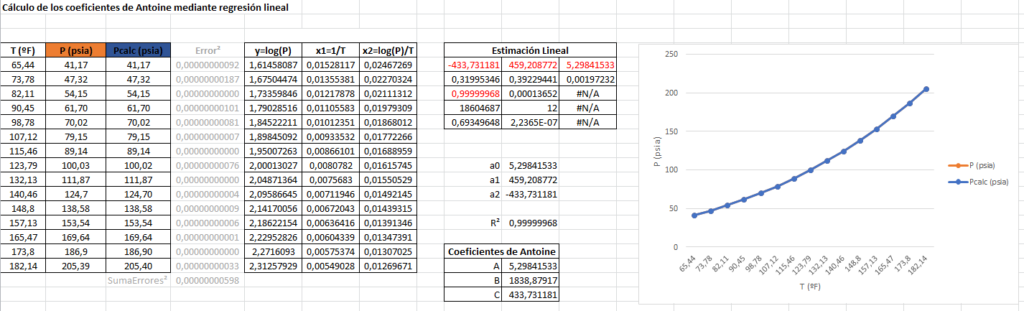
Obtener los coeficientes en Excel es tan sencillo como plantear los datos y usar la función ESTIMACION.LINEAL. Con esto obtenemos los valores de a0, a1 y a2. Relacionando las ecuaciones 4 y 5 calculamos los coeficientes A, B y C de la siguiente manera.
\begin{align}
& A = a0\\
& B = a0*-a2-a1\\
& C = a2 \\
\end{align}Para comprobar que los parámetros obtenidos son correctos podemos calcular la presión en función de ellos mediante la ecuación 12 y comparar gráficamente.
\begin{align}
& Pcalc = 10^{A - B / (T + C)}
\end{align}El parámetro R², también llamado coeficiente de determinación, que nos devuelve la estimación lineal, es la relación entre el valor real y el calculado, siendo 1 la perfección, por lo que podemos concluir que los coeficientes obtenidos son buenos.
NET
La implementación en .NET de la solución lineal con la librería de Accord no supone mayor problema. Como se puede ver a continuación en el fragmento de código, el planteamiento es sencillo y apenas supone diez líneas de código.
Dim Tx, Px As Double
'inputs(x1)(x2) -> x1 = 1 / T | x2 = log10(P) / T
Dim inputs As Double()() = New Double(14)() {}
For i = 0 To 14
Tx = DGV_API.Rows(i).Cells(0).Value
Px = DGV_API.Rows(i).Cells(1).Value
inputs(i) = New Double() {1 / Tx, Math.Log10(Px) / Tx}
Next
'outputs = y -> y = log10(P)
Dim outputs As Double() = {1.615316424, 1.675711408, 1.734153592, 1.790736182, 1.845546545, 1.898666658, 1.950173521, 2.000139525, 2.048632796, 2.0957175, 2.141454129, 2.185899763, 2.229108299, 2.271130681, 2.312015089}
'
Dim ols As New OrdinaryLeastSquares()
ols.UseIntercept = True
Dim regression As MultipleLinearRegression = ols.Learn(inputs, outputs)
'
Dim a1 As Double = regression.Weights(0)
Dim a2 As Double = regression.Weights(1)
Dim a0 As Double = regression.Intercept
' y = a0 + a1*x1 + a2*x2
Dim predicted As Double() = regression.Transform(inputs)
Dim Serror As Double = New SquareLoss(outputs).Loss(predicted)
Dim r2 As Double = New RSquaredLoss(2, outputs).Loss(predicted)
'Resultados
A = a0
B = (a0 * Math.Abs(a2) - a1)
C = Math.Abs(a2)
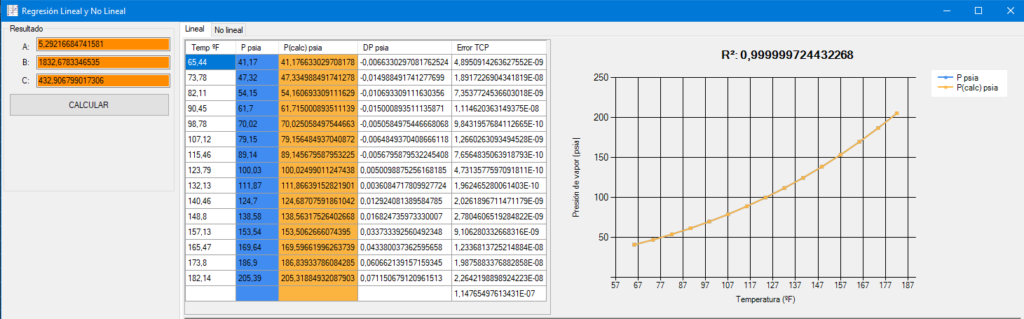
Tanto los coeficientes de Antoine como el parámetro R² son similares a los ofrecidos por Excel.
Regresión No Lineal
Excel
La única dificultad para resolver un problema de regresión no lineal con Excel radica en plantear el problema correctamente y tener activado el complemento Solver. Nuestro planteamiento parte del cálculo de una presión (Pcalc) que debe ser igual o lo más parecido posible a la presión de nuestra tabla (P). Simplificando, lo que buscamos es minimizar el error de la diferencia entre P y Pcalc alterando los coeficientes de Antoine A, B y C. Pcalc se calcula como anteriormente mediante la ecuación 12 y para el error, en realidad se utiliza el cuadrado del error, y he obtenido mejores resultados con la ecuación 14 que con la 13.
\begin{align}
& (P-Pcalc)^2\\
& (A-B / (T + C))-log(P))^2
\end{align}NET
La implementación de la regresión no lineal mediante la librería de Accord no es muy compleja pero con respecto a Excel tiene una pequeña diferencia, y es que nos obliga a plantear la función y el gradiente de la función. El gradiente es un vector que se construye mediante las derivadas parciales de cada parámetro. Que no cunda el pánico, si no te apetece coger lápiz y papel, se pueden obtener las derivadas online con WolframAlpha de forma muy rápida e intuitiva.
Dim Tx, Px As Double
'inputs(T)(-)
Dim inputs As Double()() = New Double(14)() {}
Dim output As Double() = New Double(14) {}
For i = 0 To 14
Tx = DGV_API_NL.Rows(i).Cells(0).Value
Px = DGV_API_NL.Rows(i).Cells(1).Value
inputs(i) = New Double() {Tx, 0}
output(i) = Px
Next
' Create a Nonlinear regression using LevenbergMarquardt algorithm
Dim nls As NonlinearLeastSquares = New NonlinearLeastSquares
With nls
.NumberOfParameters = 3 'A, B, C
' Initialize to some random values
.StartValues = {CDbl(Txt_A_ini.Text), CDbl(Txt_B_ini.Text), CDbl(Txt_C_ini.Text)}
'
' y = 10^(A-B / (T+C))
.Function = Function(par, inp) 10 ^ (par(0) - par(1) / (inp(0) + par(2)))
'
'Derivative in respect to the weights | Derivadas parciales
.Gradient = Sub(par, inp, result)
result(0) = Math.Log(10) * 10 ^ (par(0) - par(1) / (inp(0) + par(2))) ' d/dA
result(1) = -Math.Log(10) * 10 ^ (par(0) - par(1) / (par(2) + inp(0))) ' d/dB
result(2) = (par(1) * Math.Log(10) * 10 ^ (par(0) - par(1) / (par(2) + inp(0)))) / (par(2) + inp(0)) ^ 2 ' d/dC
End Sub
End With
'
Dim algorithm As LevenbergMarquardt = New LevenbergMarquardt
With algorithm
.MaxIterations = CInt(Txt_iter.Text)
.Tolerance = 0
End With
'
nls.Algorithm = algorithm
'
Dim regression As NonlinearRegression = nls.Learn(inputs, output)
' Use the function to compute the input values
Dim predict As Double() = regression.Transform(inputs)
' The solution will be at
A = regression.Coefficients(0) & vbNewLine
B = regression.Coefficients(1) & vbNewLine
C = regression.Coefficients(2) & vbNewLine
Resultados y Conclusiones
| Excel lineal | Excel no lineal (GRG) | .NET lineal | .NET no lineal (LM) | |
| A | 5,2984 | 4,8213 | 5,2921 | 4,9822 |
| B | 1838,8791 | 1348,0797 | 1832,6783 | 1497,0177 |
| C | 433,7311 | 354,4275 | 432,9067 | 378,3875 |
| SumaErrores² | 5,98×10-9 | 6,44×10-5 | 1,14×10-7 | 5,39×10-5 |
| R² | 0,99999968 | – | 0,99999972 | – |
La parte de la regresión lineal no tiene mayor complicación y tanto en Excel como en NET son fáciles y rápidos de implementar.
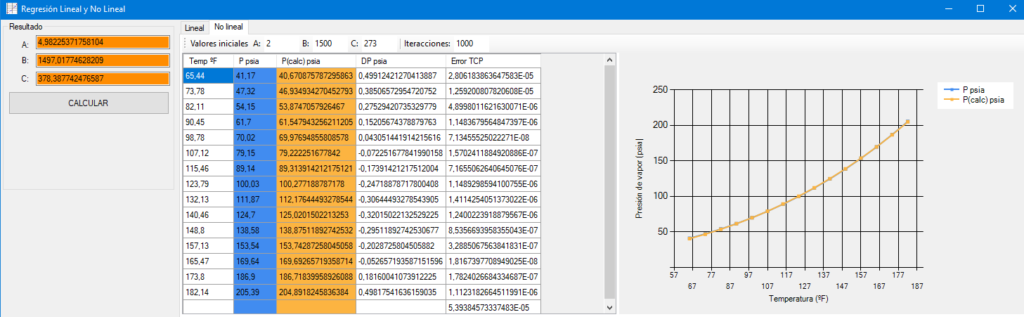
La parte de regresión no lineal no es que sea muy compleja ya que tanto Excel como Accord nos lo ponen bastante fácil, pero si es cierto que requiere que pongamos algo más de nuestra parte para obtener buenos resultados. Los algoritmos de optimización no lineal usados no han sido los mismos, Solver de Excel utiliza el algoritmo GRG (Gradiente Reducido Generalizado) y Accord dispone de los algoritmos Gauss-Newton y Levenberg-Marquardt, siendo éste último el implementado. Estos algoritmos son similares y ambos nos devuelven un mínimo local, es decir, no te dan la mejor solución pero sí una muy próxima. Estos algoritmos necesitan que les indiquemos unos valores iniciales de los parámetros o coeficientes que va a alterar para buscar una solución, y la solución obtenida depende de esos valores iniciales, por lo que tanto en Excel como en NET se ha partido de los valores 2, 1500, 273 para A, B y C respectivamente.
En general Excel es una gran herramienta que facilita el trabajo enormemente y de la que podemos sacar chispas en nuestro día a día, pero me apetecía darle una vuelta a la posibilidad de resolver problemas de optimización con un lenguaje de programación y palpar cuan fácil es obtener «eso» que con Excel se obtiene tan rápido. Espero que os sirvan los ejemplos y que los disfrutéis tanto como yo.
Descargas
Referencias
Enlaces
- Ecuación de Antoine
- Accord.NET Machine Learning Framework
- Accord.NET Ordinary Least Squares Class
- Accord.NET Non Linear Regrassion Class
- Curve fitting data to an Antoine Equation
- R-squared Is Not Valid for Nonlinear Regression
- Algoritmo Levenberg-Marquardt
- El gradiente
- GRG nonlinear
- WolframAlpha
Libros
[1] Mathias Brandewinder. Machine Learning Projects for .NET Developers, Apress. e-ISBN: 978-1-4302-6766-9
[2] David G. Luenberger, Yinyu Ye. Linear and Nonlinear Programming, Springer, e-ISBN: 978-0-387-74503-9