Optimización de redes logísticas y procesos industriales mediante IBM ILOG CPLEX

Optimización de redes logísticas y procesos industriales mediante IBM ILOG CPLEX

Comentarios 0 comentarios

Introducción

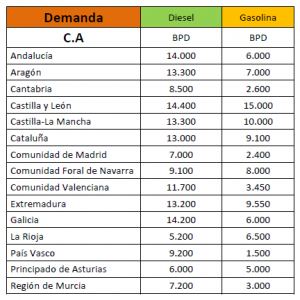
Una Empresa Petrolífera dispone de 5 refinerías repartidas por la península con una capacidad conjunta de  procesado de 770.000 barriles por día (BPD). Tras garantizar el estocaje estratégico y los bombeos para CLH, todavía disponen de 320.000 BPD para libre distribución según indica la tabla 1.

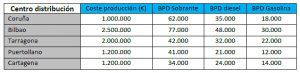
Tabla 1 – BPD según centro de distribución
Tabla 1 – BPD según centro de distribución
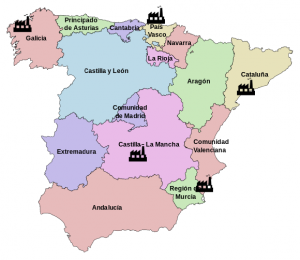
Imagen 1 – Situación de las refinerías
Imagen 1 – Situación de las refinerías

El transporte se realizará a la red de gasolineras de las diferentes comunidades autónomas (exceptuando Islas Baleares, Islas Canarias, Ceuta y Melilla) mediante la flota de camiones cisterna propia de la compañía.

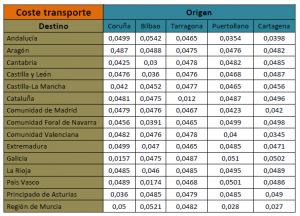
El gerente de la compañía ha solicitado un informe de optimización de transporte según el criterio de demanda de las diferentes comunidades autónomas y el coste del transporte.

Tabla 2 – Demanda actual
Tabla 2 – Demanda actual
Tabla 3 – Coste del transporte
Tabla 3 – Coste del transporte

Modelo matemático

El objetivo es minimizar costes cumpliendo con la demanda, donde:

  • RF: Refinería.
  • CA: Comunidad autónoma.
  • CosteP: Coste de la producción.
  • CosteT: Coste del transporte.
  • RFOrigen: Refinería de origen.
  • DemandaporRF: Demanda por refinería.

A continuación debemos plantear las restricciones que nos plantean la demanda y la capacidad.

Modelo OPL

Archivo .mod

/*********************************************
 * OPL 12.6.0.0 Model
 * Author: GMM
 * Creation Date: Jan/2016
 *********************************************/
//Índices
{string} Productos =…;
{string} RF =…; //Refinería
{string} CA =…; //Comunidad Autónoma

// Datos
float Demanda[CA][Productos] =…;
float CosteP [RF] =…;
float CosteT[RF][CA] =…;
float Capacidad_RFd [RF] =…;
float Capacidad_RFg [RF] =…;

// Variables
dvar float+ DemandaporRF[CA][RF][Productos];
dvar boolean RFOrigen[RF];

// Función Objetivo
minimize 
sum(r in RF) CosteP[r] * RFOrigen[r] + 
sum(c in CA, r in RF, p in Productos) CosteT [r][c]*DemandaporRF[c][r][p];

//Restricciones
subject to {
  forall (c in CA, p in Productos)
    sum(r in RF) DemandaporRF[c][r][p] == Demanda [c][p];
  forall (r in RF)
    sum (c in CA, p in Productos) DemandaporRF[c][r][p]<= (Capacidad_RFd [r] *    RFOrigen[r]) + (Capacidad_RFg [r] * RFOrigen[r]);
}

Si el planteamiento del modelo matemático lo hacemos bien, la función objetivo es fiel. Como resultado final, obtenemos el coste de la distribución desde el almacén óptimo.

  • Modelo matemático

  • Función objetivo
minimize sum(r in RF) CosteP[r] * RFOrigen[r] + sum(c in CA, r in RF, p in Productos) CosteT [r][c]*DemandaporRF[c][r][p];

Las restricciones hacen referencia a la demanda y a la capacidad.

subject to {
forall (c in CA, p in Productos)
sum(r in RF) DemandaporRF[c][r][p] == Demanda [c][p];
forall (r in RF)
          sum (c in CA, p in Productos) DemandaporRF[c][r][p]<= (Capacidad_RFd [r] *    RFOrigen[r]) + (Capacidad_RFg [r] * RFOrigen[r]);
forall (r in RF)
RFOrigen[r]<=1;
}
  • La restricción de la demanda exige que para todas las comunidades autónomas y productos, la demanda debe ser satisfecha para la refinería seleccionada.
...
forall (c in CA, p in Productos)
          sum(r in RF) DemandaporRF[c][r][p] == Demanda [c][p];
...
  • La restricción de la capacidad exige que la demanda desde cada refinería a cada comunidad autónoma y de cada producto, no supere la capacidad de dicha refinería.
...
forall (r in RF)
          sum (c in CA, p in Productos) DemandaporRF[c][r][p]<= (Capacidad_RFd [r] *    RFOrigen[r]) + (Capacidad_RFg [r] * RFOrigen[r]);
...

Archivo de datos

Archivo .dat

//Conexión con la hoja de cálculo
SheetConnection sheet("RedLogistica01.xlsx");
// Datos de la hoja Excel
Productos from SheetRead(sheet,"Hoja1!A2:A3");
RF from SheetRead(sheet,"Hoja1!A6:A10");
CA from SheetRead(sheet,"Hoja1!A14:A28");
Demanda from SheetRead(sheet,"Hoja1!B14:C28");
CosteP from SheetRead(sheet,"Hoja1!B6:B10");
Capacidad_RFd from SheetRead(sheet,"Hoja1!C6:C10");
Capacidad_RFg from SheetRead(sheet,"Hoja1!D6:D10");

Conexión con Excel

Debido a que se manejan numerosos datos, utilizaremos una hoja Excel con el fin de agilizar el proceso. La hoja Excel se llama RedLogistica01.xlsx y se encuentra en la misma ruta que el modelo y el archivo de datos. Primeramente se establece conexión para posteriormente indicarle a CPLEX los rangos de celdas que contienen los datos.

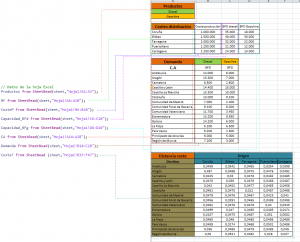
Imagen 2 – Relación Hoja de datos y Excel
Imagen 2 – Relación Hoja de datos y Excel

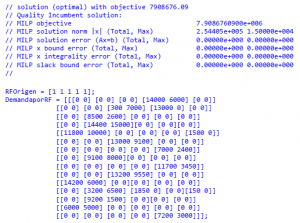
Solución OPL

Cplex arroja un coste optimizado de 7.908.676,09€. También nos indica que todas las refinerías transportarán algo mediante la variable RFOrigen y nos detalla los envíos mediante la variable DemandaporRF. Ya que en esta solución los datos no se ven correctamente, pasaremos a analizarlos en el siguiente apartado.

Interpretación de la solución

Podemos obtener la relación de orígenes y destinos mediante la vista de datos de la variable DemandaporRF como refleja la tabla 4.

Imagen 3 – Botón vista de datos
Imagen 3 – Botón vista de datos
CA (tamaño 15)RF (tamaño 5)Productos (tamaño 2)Valor
Castilla y LeónBilbaoGasolina15000
Castilla y LeónBilbaoDiesel14400
GaliciaCoruñaDiesel14200
AndalucíaPuertollanoDiesel14000
ExtremaduraTarragonaDiesel13200
CataluñaTarragonaDiesel13000
AragónPuertollanoDiesel13000
Castilla-La ManchaCoruñaDiesel11800
Comunidad ValencianaCartagenaDiesel11700
Castilla-La ManchaCoruñaGasolina10000
ExtremaduraTarragonaGasolina9550
País VascoBilbaoDiesel9200
Comunidad Foral de NavarraBilbaoDiesel9100
CataluñaTarragonaGasolina9100
CantabriaBilbaoDiesel8500
Comunidad Foral de NavarraBilbaoGasolina8000
Región de MurciaCartagenaDiesel7200
Comunidad de MadridCartagenaDiesel7000
AragónTarragonaGasolina7000
La RiojaBilbaoGasolina6500
Principado de AsturiasCoruñaDiesel6000
GaliciaCoruñaGasolina6000
AndalucíaPuertollanoGasolina6000
Principado de AsturiasCoruñaGasolina5000
Comunidad ValencianaCartagenaGasolina3450
La RiojaBilbaoDiesel3200
Región de MurciaCartagenaGasolina3000
CantabriaBilbaoGasolina2600
Comunidad de MadridCartagenaGasolina2400
La RiojaTarragonaDiesel1850
País VascoBilbaoGasolina1500
Castilla-La ManchaCartagenaDiesel1500
AragónTarragonaDiesel300
La RiojaCartagenaDiesel150
Región de MurciaPuertollanoGasolina0
Región de MurciaPuertollanoDiesel0
Región de MurciaTarragonaGasolina0
Región de MurciaTarragonaDiesel0
Región de MurciaBilbaoGasolina0
Región de MurciaBilbaoDiesel0
Región de MurciaCoruñaGasolina0
Región de MurciaCoruñaDiesel0
Principado de AsturiasCartagenaGasolina0
Principado de AsturiasCartagenaDiesel0
Principado de AsturiasPuertollanoGasolina0
Principado de AsturiasPuertollanoDiesel0
Principado de AsturiasTarragonaGasolina0
Principado de AsturiasTarragonaDiesel0
Principado de AsturiasBilbaoGasolina0
Principado de AsturiasBilbaoDiesel0
País VascoCartagenaGasolina0
País VascoCartagenaDiesel0
País VascoPuertollanoGasolina0
País VascoPuertollanoDiesel0
País VascoTarragonaGasolina0
País VascoTarragonaDiesel0
País VascoCoruñaGasolina0
País VascoCoruñaDiesel0
La RiojaCartagenaGasolina0
La RiojaPuertollanoGasolina0
La RiojaPuertollanoDiesel0
La RiojaTarragonaGasolina0
La RiojaCoruñaGasolina0
La RiojaCoruñaDiesel0
GaliciaCartagenaGasolina0
GaliciaCartagenaDiesel0
GaliciaPuertollanoGasolina0
GaliciaPuertollanoDiesel0
GaliciaTarragonaGasolina0
GaliciaTarragonaDiesel0
GaliciaBilbaoGasolina0
GaliciaBilbaoDiesel0
ExtremaduraCartagenaGasolina0
ExtremaduraCartagenaDiesel0
ExtremaduraPuertollanoGasolina0
ExtremaduraPuertollanoDiesel0
ExtremaduraBilbaoGasolina0
ExtremaduraBilbaoDiesel0
ExtremaduraCoruñaGasolina0
ExtremaduraCoruñaDiesel0
Comunidad ValencianaPuertollanoGasolina0
Comunidad ValencianaPuertollanoDiesel0
Comunidad ValencianaTarragonaGasolina0
Comunidad ValencianaTarragonaDiesel0
Comunidad ValencianaBilbaoGasolina0
Comunidad ValencianaBilbaoDiesel0
Comunidad ValencianaCoruñaGasolina0
Comunidad ValencianaCoruñaDiesel0
Comunidad Foral de NavarraCartagenaGasolina0
Comunidad Foral de NavarraCartagenaDiesel0
Comunidad Foral de NavarraPuertollanoGasolina0
Comunidad Foral de NavarraPuertollanoDiesel0
Comunidad Foral de NavarraTarragonaGasolina0
Comunidad Foral de NavarraTarragonaDiesel0
Comunidad Foral de NavarraCoruñaGasolina0
Comunidad Foral de NavarraCoruñaDiesel0
Comunidad de MadridPuertollanoGasolina0
Comunidad de MadridPuertollanoDiesel0
Comunidad de MadridTarragonaGasolina0
Comunidad de MadridTarragonaDiesel0
Comunidad de MadridBilbaoGasolina0
Comunidad de MadridBilbaoDiesel0
Comunidad de MadridCoruñaGasolina0
Comunidad de MadridCoruñaDiesel0
CataluñaCartagenaGasolina0
CataluñaCartagenaDiesel0
CataluñaPuertollanoGasolina0
CataluñaPuertollanoDiesel0
CataluñaBilbaoGasolina0
CataluñaBilbaoDiesel0
CataluñaCoruñaGasolina0
CataluñaCoruñaDiesel0
Castilla-La ManchaCartagenaGasolina0
Castilla-La ManchaPuertollanoGasolina0
Castilla-La ManchaPuertollanoDiesel0
Castilla-La ManchaTarragonaGasolina0
Castilla-La ManchaTarragonaDiesel0
Castilla-La ManchaBilbaoGasolina0
Castilla-La ManchaBilbaoDiesel0
Castilla y LeónCartagenaGasolina0
Castilla y LeónCartagenaDiesel0
Castilla y LeónPuertollanoGasolina0
Castilla y LeónPuertollanoDiesel0
Castilla y LeónTarragonaGasolina0
Castilla y LeónTarragonaDiesel0
Castilla y LeónCoruñaGasolina0
Castilla y LeónCoruñaDiesel0
CantabriaCartagenaGasolina0
CantabriaCartagenaDiesel0
CantabriaPuertollanoGasolina0
CantabriaPuertollanoDiesel0
CantabriaTarragonaGasolina0
CantabriaTarragonaDiesel0
CantabriaCoruñaGasolina0
CantabriaCoruñaDiesel0
AragónCartagenaGasolina0
AragónCartagenaDiesel0
AragónPuertollanoGasolina0
AragónBilbaoGasolina0
AragónBilbaoDiesel0
AragónCoruñaGasolina0
AragónCoruñaDiesel0
AndalucíaCartagenaGasolina0
AndalucíaCartagenaDiesel0
AndalucíaTarragonaGasolina0
AndalucíaTarragonaDiesel0
AndalucíaBilbaoGasolina0
AndalucíaBilbaoDiesel0
AndalucíaCoruñaGasolina0
AndalucíaCoruñaDiesel0

Tabla 4 – Vista de datos de la variable DemandaporRF

En la tabla 5 se puede apreciar de una forma más clara las refinerías que surten a cada comunidad autónoma. Debido al stock disponible y al coste del transporte se puede apreciar que a algunas comunidades autónomas los productos les vienen de diferentes refinerías.

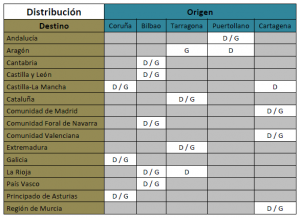
Tabla 5 – Tabla resumen de distribución
Tabla 5 – Tabla resumen de distribución

Conclusiones

Este es un pequeño ejemplo de lo que se puede conseguir optimizando un problema de redes logísticas. Hay que tener en cuenta que una refinería de media produce entre 15 y 20 productos finales y se transportan por numerosos medios, de modo que podemos encontrarnos con cientos de variables, de restricciones y con millares de datos para procesar.

Por otro lado, tanto la demanda como la oferta pueden ser variables. En este ejercicio estamos analizando la distribución del stock en un día en concreto pero la realidad es que la tabla 5 cambie a diario.

Si analizamos la producción y la demanda, vemos que la producción actual es mayor que la demanda como indica la tabla 6.

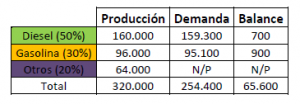
Tabla 6 – Balance
Tabla 6 – Balance

Si la demanda se incrementa o la producción disminuye el problema nos indicaría que no hay solución posible, y en una situación real habría que buscar la manera de surtir a ciertas comunidades autónomas hasta tener  de nuevo un balance positivo. En caso contrario, el sobrante se puede aprovechar para la venta en otros mercados o simplemente en procesos sucesivos ajustar la producción a la baja.

Enlaces y Bibliografía

[1] A. García Romero, M. Mena Jiménez, A. Soto Rebollo. Planificación y optimización de redes logísticas de transporte. Proyecto de sistemas informáticos [en línea]. Madrid, 2012. Disponible en: https://goo.gl/BaKLAo

[2] IBM ILOG CPLEX Optimization Studio

[3] J. J. Ruz. Tema7. Optimización de redes logísticas. Apuntes del profesor [en línea]. Madrid, 2015. Disponible en: https://goo.gl/Jafht4

[4] J. J. Ruz. Tema8. Optimización de procesos industriales. Apuntes del profesor [en línea]. Madrid, 2015. Disponible en: https://goo.gl/LvPPHP

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Información básica sobre protección de datos
Responsable Garikoitz Martínez Moreno +info...
Finalidad Gestionar y moderar tus comentarios. +info...
Legitimación Consentimiento del interesado. +info...
Destinatarios Automattic Inc., EEUU para filtrar el spam. +info...
Derechos Acceder, rectificar y cancelar los datos, así como otros derechos. +info...
Información adicional Puedes consultar la información adicional y detallada sobre protección de datos en nuestra página de política de privacidad.